zadanie optymalizacyjne paweł: Do pewnej liczby a dodano jej kwadrat,a następnie odjęto sześcian liczby a.Czy istnieje taka liczba a dla której wartość otrzymanego wyrażenia jest największa jeśli a ∊R. Wiem jaki ma byc wynik ale tego nie rozumiem. Nie wiem dlaczego.

pigor: ...., wychodzi mi, że istnieje i jest nią − tak na szybko − liczba a= ¹₃.....

ICSP: jak dla mnie nie istnieje, ponieważ lim_{x → −∞} = ∞

Mila: Nie istnieje.

vaultboy: szukam max{a+a²−a³,a∊R} f(a)=a+a²−a³ Chyba blef w treści, bo lim a→∞ f(a)=−∞ oraz lim a→(−∞) f(a)=∞ Zatem nie istnieje liczba a dla której wartość f(a) jest największa

Mila: Może czegoś w treści nie dopisano, jakieś ograniczenia?

paweł: Nie nie, jest tak jak napisałem. Piogor, masz racje ale wtedy kiedy a nalezy (0,+∞)

Mila: Właśnie o takim ograniczeniu pisałam, a∊R₊ .

paweł: Nie kapuje dlaczego tak, Jest podany tylko że a nalezy do R. Bez żadnego plusa. Ale nie rozumiem, skąd ta granica.

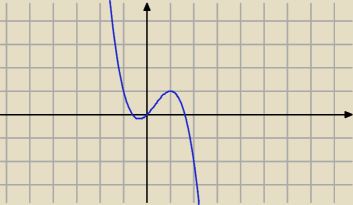
Mila: f(a)=a+a²−a³ − funkcja określona dla a∊R Badając przebieg zmienności funkcji liczysz granice na krańcach dziedziny

	1		1
lima→−∞(a+a2−a3)=a3*(		+		−1)=∞
	a2		a

	1		1
lima→∞(a+a2−a3)=a3*(		+		−1)=−∞
	a2		a

Funkcja nie jest ograniczona z góry ani z dołu. f'(a)=1+2a−3a² Liczymy miejsca zerowe f(a) −3a²+2a+1=0 Δ=16

	1
a=1 lub a=−
	3

	1
f'(a)>0 ⇔a∊(−		,1) w tym przedziale f(a) jest rosnąca
	3

	1
dla a=−		funkcja f(a) ma minimum lokalne, dla a=1 ma maksimum lokalne.
	3

f(1)=1