vaultboy:
Odp: W dowolnej konfiguracji istnieje taki trójkąt.
Dowód:
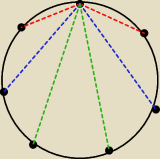
Opiszmy na tym siedmiokącie okrąg. Niech punkty na rysunku będą wierzchołkami.
Z Zasady Szufladkowej Dirichleta wynika, że istnieją co najmniej 4 wierzchołki jednego koloru
(bez straty ogólności czarnego). Zauważmy, że odległość dwóch dowolnych wierzchołków może być
długości czerwonej, niebieskiej lub zielonej (Wydaję mi się, że to widać). Mamy co najmniej 4
punkty czarnego koloru. Zatem z ZSD (znowu) pewne dwie pary punktów czarnych, będą miały tę
samą długość
(Par jest w sumie 6, a długości są tylko 3), to oznacza, że pewne dwa boki są równe czyli
dostajemy szukany trójkąt równoramienny.
 Odp: W dowolnej konfiguracji istnieje taki trójkąt.
Dowód:
Opiszmy na tym siedmiokącie okrąg. Niech punkty na rysunku będą wierzchołkami.
Z Zasady Szufladkowej Dirichleta wynika, że istnieją co najmniej 4 wierzchołki jednego koloru
(bez straty ogólności czarnego). Zauważmy, że odległość dwóch dowolnych wierzchołków może być
długości czerwonej, niebieskiej lub zielonej (Wydaję mi się, że to widać). Mamy co najmniej 4
punkty czarnego koloru. Zatem z ZSD (znowu) pewne dwie pary punktów czarnych, będą miały tę
samą długość
(Par jest w sumie 6, a długości są tylko 3), to oznacza, że pewne dwa boki są równe czyli
dostajemy szukany trójkąt równoramienny.
Odp: W dowolnej konfiguracji istnieje taki trójkąt.
Dowód:
Opiszmy na tym siedmiokącie okrąg. Niech punkty na rysunku będą wierzchołkami.
Z Zasady Szufladkowej Dirichleta wynika, że istnieją co najmniej 4 wierzchołki jednego koloru
(bez straty ogólności czarnego). Zauważmy, że odległość dwóch dowolnych wierzchołków może być
długości czerwonej, niebieskiej lub zielonej (Wydaję mi się, że to widać). Mamy co najmniej 4
punkty czarnego koloru. Zatem z ZSD (znowu) pewne dwie pary punktów czarnych, będą miały tę
samą długość
(Par jest w sumie 6, a długości są tylko 3), to oznacza, że pewne dwa boki są równe czyli
dostajemy szukany trójkąt równoramienny.