 1)
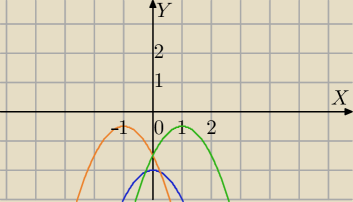
wykres f(x)=(p2−4)x2+2px−1 musi leżeć pod osią OX, czyli
p2−4<0 ( parabola skierowana w dół) i Δ<0 (brak miejsc zerowych)
Masz przykłady na rysunku.
2) dla p2−4=0 mamy p=2 lub p=−2 wtedy:
f(x)=0*x2+4x−1
f(x)=4x−1 funkcja liniowa przyjmuje wartości dodatnie i ujemne
lub
f(x)=−4x−1funkcja liniowa przyjmuje wartości dodatnie i ujemne
Zatem zostają tylko warunki:
(p−2)*(p+2)<0 i Δ=4p2+4*(p2−4)<0⇔
p∊(−2,2) i 8p2−16<0 /:8
dokończysz sam?
1)
wykres f(x)=(p2−4)x2+2px−1 musi leżeć pod osią OX, czyli
p2−4<0 ( parabola skierowana w dół) i Δ<0 (brak miejsc zerowych)
Masz przykłady na rysunku.
2) dla p2−4=0 mamy p=2 lub p=−2 wtedy:
f(x)=0*x2+4x−1
f(x)=4x−1 funkcja liniowa przyjmuje wartości dodatnie i ujemne
lub
f(x)=−4x−1funkcja liniowa przyjmuje wartości dodatnie i ujemne
Zatem zostają tylko warunki:
(p−2)*(p+2)<0 i Δ=4p2+4*(p2−4)<0⇔
p∊(−2,2) i 8p2−16<0 /:8
dokończysz sam?