 Pomocy, mam obliczyć całkę podwójną (za pomocą zmiennych biegunowych)
Pomocy, mam obliczyć całkę podwójną (za pomocą zmiennych biegunowych) Mam taką całkę
∫∫xydxdy po D:x2+y2<=1, x√3<=y<=√3x
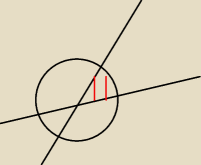
Problem w tym że nie wiem jak obliczyć D. Do tej pory doszłam do rysunku z góry. Ale nie mam
pojęcia co dalej, jak obliczyć D z tego czerwonego obszaru?
Mam taką całkę
∫∫xydxdy po D:x2+y2<=1, x√3<=y<=√3x
Problem w tym że nie wiem jak obliczyć D. Do tej pory doszłam do rysunku z góry. Ale nie mam
pojęcia co dalej, jak obliczyć D z tego czerwonego obszaru?

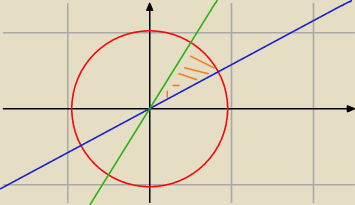 Wyznaczasz kąt nachylenia niebieskiej prostej, oraz kąt nachylenia prostej zielonej. Wtedy :
wyznaczony kąt ≤ α ≤ wyznaczony kąt
Wyznaczenie przedziału r jest jeszcze prostsze.
Promienie są jeszcze prostsze. Pomyśl.
Wyznaczasz kąt nachylenia niebieskiej prostej, oraz kąt nachylenia prostej zielonej. Wtedy :
wyznaczony kąt ≤ α ≤ wyznaczony kąt
Wyznaczenie przedziału r jest jeszcze prostsze.
Promienie są jeszcze prostsze. Pomyśl.
| rcosα | |
≤rsinα≤√3rcosα⇔ | |
| √3 |
| cosα | |
≤sinα≤√3cosα | |
| √3 |
| √3 | |
≤tgα≤√3 | |
| 3 |
| π | π | ||
≤α≤ | |||
| 6 | 3 |

 Dzięki wielkie, naprawdę
Dzięki wielkie, naprawdę 