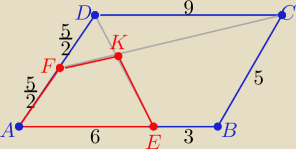
czworokąt Eta: Oblicz pole czworokąta AFKE (rys.)

Kacper: Dla kogo to zadanie Eta?

Eta: Dla chętnych

Eta: Zapomniałam jeszcze dopisać,że kąt ostry równoległoboku ma miarę 60^o

Kacper: No właśnie robię rysunek i czegoś mi brakowało

Eta: Jak tam Kacper

Kacper: Pytasz czy zrobiłem?

Eta: tak

Kacper: Mam jakiś pomysł, ale straszny rachunkowo. A zapewne liczy sie prosto

Eta: To myśl dalej

Metis: 2 razy cosinusów? Czy 2 razy Piatagorasem?

Eta:

Eta: Ładne zadanko kto chętny?

Kacper: Daj mi jeszcze chwilę, bo myślę nad tym jak je zrobić bez brutalnych metod

Eta: Ok ja mam czas, ja poczekam

Karolina96: Odcinek |FK| to 1/3 FC

Kacper: Ja muszę lecieć, bo mam inne obowiązki, ale o zadaniu pamiętam Brakuje mi jednego elementu i zadanie robi się w pamięci

Eta:

Eta:

Kacper: Chyba mam

Eta: Jaka odp: ?

Kacper: Oficjalnie wynik to:

195√3
32

Ale muszę przyznać, że się namęczyłem Rachunki proste, tylko wymyśleć trudno

Kacper: Eta powiedz, że dobrze

Eta:

Kacper: Napisze ci na maila rozwiązanie, bo może ktoś jeszcze będzie chciał robić Ciekaw jestem czy jest krótsza droga od mojej

Eta: ok czekam

Hugo: ta teoria + pitagora sporo układów równan i wyliczyc ?

Bogdan: Wystarczy zastosować twierdzenia: Talesa i sinusów, nie ma układów równań.

Eta:

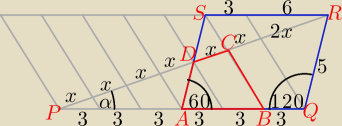
Bogdan: Oznaczenia: |CD| = x, |∡BPC| = |∡APD| = α |AD| = |DS| Korzystając z twierdzenia Talesa wnioskujemy, że |PD| = 4x i |PC| = 5x. Z twierdzenia sinusów w trójkącie PQR otrzymujemy:

8x		5		5√3
	=		⇒ sinα =
sin120o		sinα		16x

Pole czworokąta ABCD:

	1		1		39x		5√3
P = PBPC − PAPD =		*5x*15*sinα −		*4x*9*sinα =		*
	2		2		2		16x

	195√3
Ostatecznie P =
	32

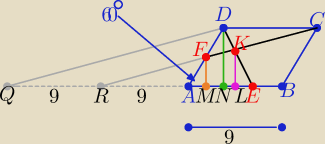
Eta: P=P(RKE)− P(RFA) FM , DN, KL −−−− trzy wysokości poprowadzone na bok AB

	5		5√3		5√3
|QE|=24, |RE|=15 , |FM|=		*sin60o=		, |DN|=5*sin60o=
	2		4		2

Z podobieństwa trójkątów QDE i RKE :

|QE|		|DN|		8		5√3		25√3
	=		⇒		=		⇒ |KL|=
|RE|		|KL|		5		2|KL|		16

	1		25√3		1		5√3		375√3		180√3
P=		*15*		−		*9*		=		−		=
	2		16		2		4		32		32

	195√3
P=
	32

Saizou : wystarczy w sumie tylko podobieństwo trójkątów

Eta: @ Saizou To podaj swoje rozwiązanie

Saizou : Można się jeszcze inaczej pobawić, może jutro pokażę moje rozwiązanie

wieszcz : bohdan skad takie podzielenie tego rownolegloboku mozesz wytlumaczyc albo dac jakas stronke do tego

Bogdan: Używam na tym forum imienia Bogdan, nie Bohdan. Taki miałem pomysł na rozwiązanie tego zadania. Nie rozumiem pytania o stronkę do tego.

wieszcz : ok będe wiedział na przyszłość

Kacper: Ja też używałem tylko podobieństwa Napiszę w przerwie swoje rozwiązanie

Ada: wieszcz takie podzielenie to twierdzenie Talesa. Stronka→http://pl.wikipedia.org/wiki/Twierdzenie_Talesa

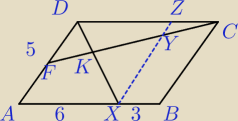
Kacper: odcinek XZ − równoległy do boków AD i BC. ΔCYZ~CFD (skala 1/3) ΔFKD~ΔKYX (skala 3/5) Na pole równoległoboku AXZD składa się P_AXFK+P_XKY+P_KYZD+P_FKD Po kilku drobnych rachunkach otrzymujemy odpowiedź

Eta: No i mamy kilka sposobów rozwiązania tego zadania

kyrtap: a kogo najlepszy?

Eta: A kogo ? ........... piszemy : "a czyj sposób najlepszy" ?

kyrtap: chłop z Mazur nie zna się na poprawnej polszczyźnie

Eta:

kyrtap: ale dzięki że poprawiłaś

Kacper: Mnie bardzo podoba się sposób Ety

Eta:

Kacper: Ja mam zawsze problem z zadaniami, gdzie należy coś dorysować

kyrtap: ja ogólnie mam dużo problemów ^^

Hugo: dobrze ze Hugo czuwa

kyrtap: nad czym czuwasz?