nieównosci faraon : 6x≤x²

faraon : help help

faraon : ?

Janek191: Kliknij na kolor niebieski po lewej stronie na: Funkcja kwadratowa , a następnie nierówność kwadratowa

Eta: x²−6x≥0 ⇒ x(x−6) ≥0 ⇒ x∊...........

faraon : 6x≤x² to bedzie jak

PW: Be znajomości funkcji kwadratowej też da się rozwiązać. 6x ≤ x² − nierówność ta jest spełniona w sposób oczywisty, gdy x ≤ 0 (lewa strona jest niedodatnia, prawa nieujemna). Część rozwiązań już mamy: x ∊ (−∞, 0]. Poszukajmy rozwiązań dla x > 0. Po podzieleniu stronami przez x mamy nierówność: 6 ≤ x, x > 0, której rozwiązaniem jest zbiór x∊[6,∞). Dzielenie stronami przez x można było wykonać i w wyniku otrzymaliśmy równoważną nierówność o "takim samym zwrocie", gdyż x > 0. Odpowiedź: Rozwiązaniem nierówności jest zbiór (−∞, 0]∪[6,∞).

Eta: Za dużo czytania

faraon : a jak to zapisac to poprostu łatwo bez tych zdan

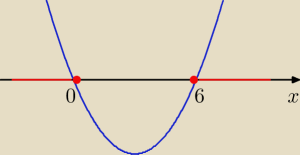
Eta: Nie widzisz na rysunku? Odp: x∊(−∞,0> U <6,∞)

faraon : dobra ale to odp a do tego są zapisy obliczenia

Eta: Wszystkie zapisy masz pod rysunkiem ... też nie widzisz?

faraon : nie

Eta: To zgłoś się do okulisty po dobre okulary

Janek191: Kolejka do okulisty ?

Eta: https://matematykaszkolna.pl/strona/100.html

PW: Wiadomo, faraon, mowa polska trudna. Ale tak prawdę mówiąc rozwiązanie Ety też wymaga myślenia. Gdybyś chciał je przedstawić bez rysunku, to byłoby: x·(x−6) ≥ 0, mamy do czynienia z iloczynem dwóch czynników. Jest on nieujemny, gdy: a) x ≥ 0 i x − 6 ≥ 0 lub b) x ≤ 0 i x − 6 ≤ 0. Rozwiązaniem układu nierówności a) są x ≥ 6, a rozwiązaniem układu b) są x ≤ 0. Odpowiedź jak wyżej, można ją popreć rysunkami zbiorów na osi. Bez pisania po polsku i bez myślenia się nie da.