Ca 52: Proste zadania a ja się gubię, liczę na waszą pomoc Oblicz całkę podwójną ∫∫ (x²+y²)dxdy gdzie D jest obszarem x²+y²≤2 D Nowy obszar U : 0≤γ≤2π 0≤r≤√2 ∫∫r²drdγ= ∫₀^√2 { ∫₀^2π r²dγ}dr=.. U ∫r²dγ=r²γ+c [r²γ]^2π₀=2πr²

	2πr3
∫2πr2=		+C
	3

	4√2π
[U{2πr3}{3]√20=
	3

Odp jest inna... Co robię źle? Pewnie wszystko... Proszę pomóżcie

Przemysław: Nie brakuje czasami jakobianu przejścia?, tzn chyba całka z r³ powinna być, ale głowy nie dam.

52: Dzięki

52: ∫∫ √x²+y²dxdy D:{(x,y): x²+y²≤2x D Wyszło mi że 0≤r≤rcosγ Jak wyznaczyć przedział dla γ ?

52: * 0≤r≤2cosγ

Godzio:

	π
γ ∊ [0,		], bo musi być zachowana nierówność r ≤ 2cosγ, a to zachodzi gdy cosγ jest
	2

nieujemny

52: Dzięki tylko jak wykładowca robił na wykładzie przykład i było 0≤r≤4cosγ to daliśmy

	π		π
γ∊[−		,		]
	2		2

Tylko że wtedy obliczaliśmy objętość bryły,ale to chyba nie wpływa na to ... Nic nie rozumiem, gubię się cały czas... bez ćwiczeń analiza to okrucieństwo

Godzio:

	π		3
No tak rzeczywiście, powinienem zapisać γ ∊ [0,		] U [		π,2π], a równoważnie jest to
	2		2

	π		π
γ∊[−		,		]. Powinno się brać pod uwagę całe kółko i z niego odczytywać granice.
	2		2

52: Nie rozumiem czemu tak ... Możesz to jakoś bardziej wyjaśnić, narysować, bo nie wiem co się dzieje Myślałem że jak mam koło to zawsze to będzie [0,2π] , a tu jednak tak nie jest chyba że Środek okręgu leży na punkcie P(0,0), tak ? Dlaczego tutaj γ jest inne ?

52: Dobra, już wiem... Głupi jestem... Dzięki Godzio

Godzio: Od środka zależy to w pewnym stopniu, ale nawet jak jest P(0,0) to nie oznacza, że będzie od [0,2π] bo zależy również od innych warunków. [0,2π] będzie zawsze jeżeli mamy kółko o środku w P(0,0) i żadnych innych warunków, jeżeli dojdą jakiekolwiek to trzeba wycinać z kółka te warunki i tutaj mamy warunek cosγ ≥ 0, a wiem, że jest od nieujemny w przedziale [0,π/2] U [3/2π,2π], ale wtedy wyjdą nam dwie całki z jednej, więc łatwiej wziąć identyczny przedział zapisany inaczej [−π/2, π/2].

52: Jeszcze raz dzięki Odpoczywasz ?

Godzio: Tak, a nie powinienem

Godzio: A co, masz coś jeszcze?

52: nom Sorry że zawracam gitarę... Obszar ograniczony tak: 1≤x²≤+y²≤2 y≥x≥0

π		5π
	≤γ≤
4		4

1≤r≤√2 co ty na to ?

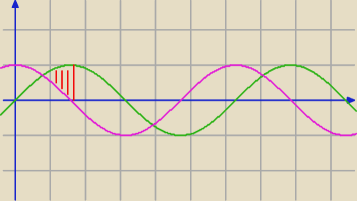
Godzio: Chyba tak: rsinγ ≥ rcosγ ≥ 0 sinγ ≥ cosγ ≥ 0

	π		π
γ ∊ [		,		]
	4		2

52: No tak samo zrobiłem i ta zielona linia (sin) jest większa od cos trochę dalej niż ty napisałeś... no nie ?

Godzio: Ale cosinus jest ujemny, a ma być nieujemny prawda?

52: a widzisz ty jednak jesteś

52: ∫xy²dxdy=... ograniczona tym obszarem wyżej

	π
...= ∫{		π/2 { ∫√21 r4cosγ sin2γ dr } dγ tak?
	4

Dobra kolejność całkowania i dobra całka w środku ?

Godzio: Kolejność w tym wypadku nie ma znaczenia, całka dobra

52: Jak to nie ma znaczenia ?

Godzio: Jeżeli masz iloczyn funkcji f(r) * f(γ) to możesz je rozdzielić na iloczyn całek, bo jedna od drugiej nie zależy, a więc i kolejność całkowania nie ma znaczenia.

52: Faktycznie, coś było Dziękuję bardzo

52: Obliczyć objętość bryły V ograniczonej powierzchniami z=y²−x², z=0, x=0, y=2 oraz y=x Nie wiem jak zacząć (Odpowiadam na pytania, tak było to, ale szybko i trochę chaotycznie) jakby ktoś poświęcił mi trochę czasu i wytłumaczył krok po kroku, byłbym baardzo wdzięczny :0

Godzio: Wiadomo co to za krzywa: z = y² − x²? Pierwsza rzecz jaką trzeba zrobić to to narysować

52: Czyli po zadaniu... nie umiem i chyba się nie nauczę rysować w R³ jakby był + to paraboloida obrotowa a tak to nie wiem

52: To jest siodło ?

Godzio: Tak, spróbuje to tutaj jakoś narysować

52: https://www.google.pl/webhp?ie=utf-8&oe=utf-8&gws_rd=cr&ei=i8RgVYXnMIm6sQHj7ID4BQ#q=z+%3D+y^2-x^2

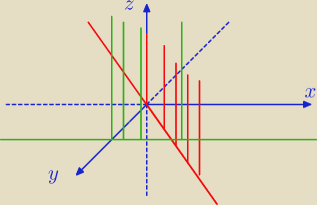
Godzio: z = 0 to płaszczyzna OXY x = 0 to płaszczyzna OZY (tych dwóch nie rysuje) y=x y=2 Widać, że wyszedł nam graniastosłup trójkątny, którego ściany boczne są ograniczone płaszczyznami y = 2, x = 0 i y = 2, a podstawa płaszczyzną z = 0 teraz to "siodło" będzie ograniczeniem górnym (albo dolnym) to muszę na kartce rozrysować, żeby to zobaczyć, momencik

52: ok, ciężko z tymi rysunkami coś czuję będzie (u mnie )

Mila: Jaki wynik?

52: Witaj Mila Wyników nie mam, bo to Pan wykładowca nam wstawił na swoją stronkę przykładowe zadania jakie mogą być na egzaminie Tutaj link http://prac.im.pwr.wroc.pl/~merdas/AM2.3.pdf

Godzio: z = y² − x² Dla x = 0 mamy z = y² Dla y = 0 mamy z = −x² No dobra, będzie górnym, zatem nasza całka powinna wyglądać tak: 2∫₀²∫₀^x∫₀^{y2 − x2}dzdydx A ta dwójką jest stąd, że po drugiej stronie jest obszar symetryczny, ale jeszcze muszę to przemyśleć, za chwilę potwierdzę

52: Dałeś całkę potrójną ?

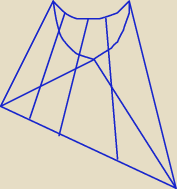
Godzio: Tak, ale nie musi być, to jest po prostu całka z y² − x² (podwójna) Moim zdaniem takie cudo wychodzi, ale niech się Mila wypowie, obawiam się, że takie rzeczy mogły mi już z głowy wylecieć.

Godzio: Ta ściana od przodu (kreskowana) jest pionowa.

52: to będzie tak : ∫²₀ dx ∫²_x (y²−x²)dy tak ? Trochę nie mam pojęcia skąd się to bierze...

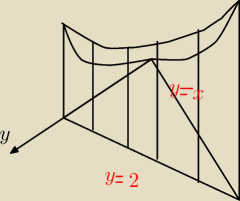
Godzio: Lepiej już nie narysuje (odwołuje dwójkę z całki)

52: Godzio rysujesz ślicznie zobacz post 20:53

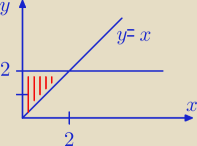
Godzio: y od x do 2 x od 0 do 2

Godzio: Teraz wiadomo skąd?

52: No tak w sumie to logiczne, wielki dzięki Macie może jakieś zadania (proste do przećwiczenia wraz z odpowiedziami) ?

52: Takie łatwe rzeczy, a ja je utrudniam

Godzio: Oblicz objętość brył ograniczonych: a) x² + y² − 2y = 0 , z = x² + y², z = 0

	3
Odp:		π
	2

b) (x − 1)² + (y − 1)² =1, z = xy, z = 0 Odp: π

Godzio: Czyja wiem, czy takie łatwe

52: na wsp. biegunowe... no pięknie No dobra łatwe, może to nie jest, ale czasami co ja wyczyniam to się w głowie nie mieści

52: Godzio zrobimy a) ?

52: x²+y²−2y=0 S(0,1) r=1 x²+y²=2y r=2sinγ 0≤γ≤π 0≤r≤2sinγ a z tego zrobiłem z=x²+y² z=r² ... ale to bez sensu

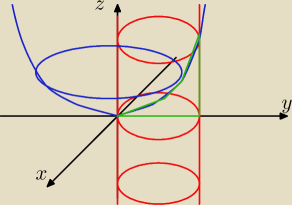
Godzio: Uczmy się przy okazji to rysować (w potrójnych się przyda ) x² + (y − 1)² = 1 −− okrąg o środku w (0,1) i promieniu 1. teraz 'z' zmienia się dowolnie więc mamy nieskończony walec. Teraz z = x² + y² −− paraboloida z ramionami do góry. z = 0 płaszczyzna OXY ∫∫x² + y²dxdy przy warunku x² + y² = 2y r = 2sinγ,

	16sin4γ		3
∫0π∫02sinγr3drdγ = ∫0π		dγ = 4∫0πsin4γdγ =		π
	4		2

Godzio: A co Ci się wydawało bez sensu?

52: To dobrze zrobiłem ! tylko nie uzględniłem 4 Ekstra Dzięki wielkie

52:

	3π
Bo doszedłem do postaci 4∫2sinγ0 sin4γ dγ i wyszło mi		a zapomniałem że 4 z
	8

przodu..

52: http://www.zadania.info/d64/322337 nie ma prostszego sposobu na tą całkę ?

Godzio: Obawiam się, że nie, ja zawsze nim robię.

52: Ok

Mila: To chyba najprostszy. Raczej zapamiętaj wzór : cos(2x)=cos²x−sin²x i jego dwie inne wersje: cos(2x)=2cos²x−1 i cos(2x) =1−2sin²x To często przydaje się w całkach trygonometrycznych.

52: Ok dzięki teraz b) Kosmos... z tego (x−1)²+(y−1)²=1

	π
0≤γ≤
	2

	1
0≤r≤cosγ+sinγ+2sin		γ
	2

dobrze ?

b.: 52, 23 maj 2015 22:25: jest prostszy sposób,

	eix−e−ix		e4ix − 4e2ix + 6 − 4e2ix + e−4ix
sin4x = (		)4 =		=
	2i		16

	cos4x		cos2x		3
		−		+		,
	8		2		8

a to się już łatwo całkuje.

52: że na to nie wpadałem to nie ja nie wiem

Godzio: Może lepiej tak: x − 1 = rcosγ y − 1 = rsinγ r ∊ [0,1] γ ∊ [0,2π]

52: W życiu bym na to nie wpadł... Za trudne Godzio dałeś

Godzio: Zawsze chcesz, żeby się uprościło Jeżeli jest warunek (x − a)² + (y − b)² = c² to się narzuca (o ile w całce jest coś innego niż x² + y²) podstawienie x − a = rcosγ y − b = rsinγ r ∊ [0,c], c > 0 γ ∊ [0,2π]

52: Dzięki, w sumie analizę nawet by się jakoś ogarnęło ładnie, jakby nie było innych kursów Jeszcze raz dzięki wszystkim