Równania z wartoscia bezwzględna rafciooo: Witam. Mam pytanie. Jestem w trakcie robienia pewnego zadania i potrzebuję pomocy: x∊<−1,2> −x + 2 + x + 1 < 5 0x < 2 To jaki powinien być wynik? Cały ten zbiór czy tylko x∊<−1,2) ?

Przemysław: Wg mnie x∊<−1,2), bo oba warunki naraz. Ale mogę się oczywiście mylić

Mila: Sprawdź dla x=2

rafciooo: No to już sam nie wiem. Niech mi ktoś to sprawdzi najlepiej tutaj całe moje rozwiązanie: |x−2|+|x+1|<5 1. x∊<−nieskończoności,−1) −x +2 + −x + 1 < 5 −2x<4 x>−2 x∊(−2,−1) 2. x∊<−1,2> −x + 2 + x + 1 < 5 0x < 2 x∊<−1,2) 3. x∊(2,+nieskonczonosci) x −2 + x + 1 < 5 2x < 6 x < 3 x∊(2,3) A prawidłowy wynik dla całego równania to x∊(−2,3). A z moich wyników wychodzi x∊(−2,2)∪(2,3) Bardzo proszę o pomoc

Przemysław: 2. x∊<−1,2) 3 x∊<2;∞) i wtedy chyba wyjdzie to co trzeba.

	⎧	y dla y≥0
Bo |y|=	⎨
	⎩	−y dla y<0

a u Ciebie w punkcie 2. bierzesz x=2, czyli wartość bezwlędna równa 0, ale Ty korzystasz z tej części definicji, gdzie ma być ona mniejsza niż 0 (bo masz −x+2, a nie x−2). takie moje przemyślenia, może coś to da TLDR Weź te przedziały co napisałem i chyba wyjdzie co trzeba

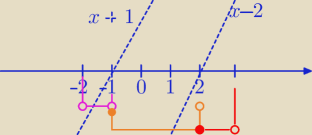
Mila: |x−2|+|x+1|<5 1) x<−1 −x+2−x−1<5 −2x+1<5 −2x<4 x>−2 x∊(−2,−1) 2) x∊<−1,2) −x+2+x+1<5 3<5 nierówność prawdziwa <−1,2) 3) x≥2 x−2+x+1<5 2x<6 x<3 x∊<2,3) odp. x∊(−2,3)