planimetria mikuś: Bardzo proszę o pomoc w rozwiązaniu zadań 1) W trójkącie równoramiennym kąt między ramionami ma miarę 20^o. Podstawa i ramiona mają długość odpowiednio a i b. Wykaż ,że zachodzi równość a³+b³=3ab² 2)W trójkącie o bokach długości a, b, c oraz kącie α między bokami b i c

	a2
zachodzi nierówność		+cosα≥1
	2bc

Mila: w (1) kąt 20^o, czy 120^o ?

mikuś: 20^o

Eta:

	a
sin10o=
	2b

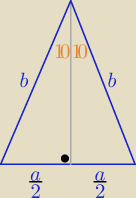
teraz korzystam ze wzoru na sin(3α)=3sinα−4sin³α

	a		a
sin30o=3*		−4*(		)3
	2b		2b

1		3a		a3
	=		−		/*2b3
2		2b		2b3

b³=3ab²−a³ ⇒ a³+b³=3ab² c.n.u

mikuś: Dziękuję A jeszcze drugie pomożesz plisss

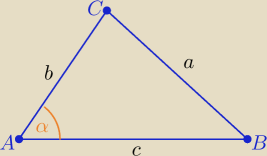
Eta: Z twierdzenia kosinusów:

	b2+c2−a2
cosα=
	2bc

Jeżeli taka nierówność zachodzi, to przekształcamy ją równoważnie

a2		b2+c2−a2
	+		≥1
2bc		2bc

b2+c2
	≥1 /*2bc>0
2bc

b²+c²≥2bc ⇔b²−2bc+c²≥0 ⇔(b−c)²≥0 , dla b=c zachodzi równość

	a2
to nierówność		+cosα≥ 1 −−− zachodzi
	2bc

c.n.u