
| 1 | ||
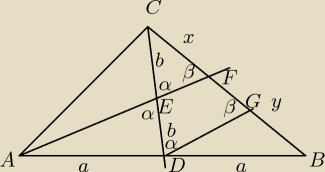
DG= | AF i DG || FA (wynika to z tw że odc łączący środki boków trójkąta jest połową boku | |
| 2 |
| 1 | ||
FG=FB = | y
| |
| 2 |
| x | b | ||||||||
= | |||||||||
| 2b |
| 1 | ||
2x = | y+x
| |
| 2 |
| 1 | ||
x= | y
| |
| 2 |
| x | 1 | ||
= | |||
| y | 2 |

| 1 | ||
DG= | AF i DG || FA (wynika to z tw że odc łączący środki boków trójkąta jest połową boku | |
| 2 |
| 1 | ||
FG=FB = | y
| |
| 2 |
 z podobieństwa FEC i DGC
z podobieństwa FEC i DGC
| x | b | ||||||||
= | |||||||||
| 2b |
| 1 | ||
2x = | y+x
| |
| 2 |
| 1 | ||
x= | y
| |
| 2 |
| x | 1 | ||
= | |||
| y | 2 |
