sss gabu: Napisz równanie okręgu o środku w punkcie: a) S= (−5,2), stycznego do prostej 2x−y+5=0 b) S= (4, −2), stycznego do jednej z osi układu wspólrzednych

===: a) (x+5)²+(y−2)²=r² i zauważ, że r jest jednocześnie odległością punktu S od danej prostej

J: a) (x+5)² + (y−2)² = r² , gdzie r promień, to odległość środka od prostej b) pomyśl... r już widać

===:

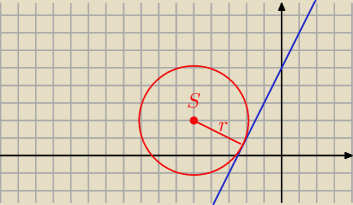
Janek191: a) S = ( − 5, 2) 2 x − y + 5 = 0 więc

	I 2*(−5) − 1*2 + 5 I		7
r =		=
	√22 + (−1)2		√5

więc

	49
r2 =
	5

Równanie okręgu:

	49
( x + 5)2 + ( y − 2)2 =
	5

==========================