Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A... basia: Pomoże; ktoś? Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A. Przez punkt P(2, 4) poprowadzono prostą l, która przecięła oś OY powyżej punktu A. Suma pól dwóch trójkątów powstałych między prostymi k, l oraz osiami układu współrzędnych jest równa 6. Napisz równanie prostej l.

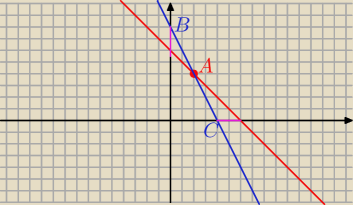
Janek191: B = ( 0, y₁) C = (x₂, 0) 0,5*( 6 − x₂)*4 + 0,5*( y₁ − 6)*2 = 6 12 − 2x₂ + y₁ − 6 = 6 2 x₂ = y₁ B = ( 0,8) C = ( 4, 0) Pr BC y = a x + b więc 8 = 0*a + b ⇒ b = 8 0 = 4a + b = 4a + 8 ⇒ a = − 2 zatem y = − 2 x + 8 =========

prosta: skąd wiemy, że x₂=4 ? zgadujemy?

Andrzej: 210γδππ≥←→⇒←→≥≥≥≥≥≤≤≤≤∞∞ΩΩΩ

Janek191: 2 x₂ = y₁

prosta: prosta l ma równanie : y=ax+y₁ i leży na niej punkt (x₂,0) stąd: ax₂+y₁=0 i y₁=2x₂ mamy więc ax₂+2x₂=0 x₂(a+2)=0 i x₂>0 a=−2 na prostej l leży punkt P(2,4) y=−2x+y₁ ⇒ −2*2+y₁=4 y₁=8 i mamy równanie prostej: y=−2x+8

basia: dziękuje!