oblicz obwód, pole, promień - rozszerzenie yvdhg: 1. Trapez ABCD o kątach ostrych 30* i 60* jest opisany na okręgu o promieniu pierwiastek z 3. Oblicz pole i obwód tego trapezu. 2. Długość jednego z boków trójkąta jest równa 6cm, a cosinus kąta leżącego przy tym boku wynosi 1/3. Oblicz promień okręgu wpisanego w ten trójkąt, jeżeli promień okręgu na nim opisanego jest równy 9cm. Bardzo bym prosił o bardzo przejrzyste rozpisanie wszystkiego (po kolei) oraz o rysunki. Zależy mi na tym, żeby to zrozumieć, a nie tylko przepisać

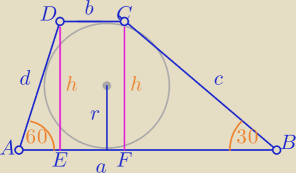
Mila: r=√3 h=2√3 a+b=c+d h=2√3 W ΔAED:

	h
sin60=
	d

√3		2√3
	=
2		d

d=4 W ΔCFB:

	h
sin30=
	c

1		2√3
	=
2		c

c=4√3 Obw=2*(4+4√3) P=p*r, p− połowa obwodu P=(4+4√3)*√3 P=4√3+12 ==============

yvdhg: o super, dziękuję bardzo! mam tylko jeszcze pytanie, bo pierwszy raz się z tym spotykam: dlaczego obwód liczmy 2*(d+c), a pole − połowę obwodu x promień? są na to jakieś wzory, czy skąd to się bierze?

yvdhg: ah oki, zapomniałem o bokach, gdy można wpisać okrąg. Już rozumiem, dziękuje bardzo gdyby ktoś potrafił drugie zadanie, byłoby bardzo miło!

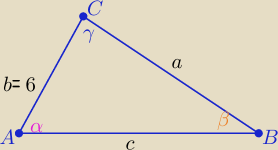
Eta: R=9

	1		1		2√2
cosα=		⇒ sinα= √1−		=
	3		9		3

z tw. sinusów: a=2R*sinα ⇒a=12√2

	6		1
sinβ=		⇒ sinβ=
	2R		3

jeżeli cosα= sinβ to trójkąt ABC jest prostokątny : γ= 90^o i c= 2R=18

	a+b−c
r=		= ........ dokończ
	2

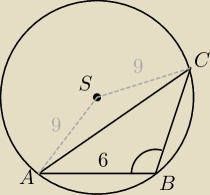
YushokU: R=9

	1
cos∡ABC=
	3

∡ASC=180−2∡ABC

	1		−8
cos∡ASC=−cos(−2∡ABC)=cos2∡ABC=2cos2∡ABC−1=		−1=
	9		9

Z tw. cosinusów. AC²=2R²(1−cos∡ASC) AC²=AB²+BC²−2AB*BC*cos∡ABC To do przyrównania, a potem mając już długości wszystkich boków.

	abc		a+b+c
P=		=r
	4R		2

Do wyliczenia, ja muszę już niestety lecieć. Dobranoc!

Eta:

Eta: Trójkąt jest prostokątny sprawdzamy: a=12√2, b= 6 , c=2R=18 a²+b²= c² : 288+36= 324 324=324 odp: r= 6(√2−1)

yvdhg: Świetnie, dziękuje wam bardzo za pomoc!