wartość najmniejsza funckji M.: Mamy parabolę o wzorze y=x² oraz punkt A (0,1). Mamy znaleźć punkt na paraboliw najmniejszej odległości od puntu A. zrobiłam założenie,że x≥0 ,ale dalej nie wiem jak sie za to zabrać ?

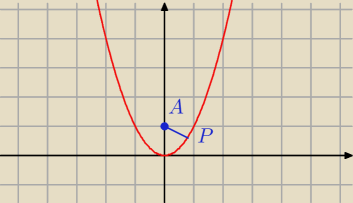
Janek191: A = ( 0, 1) P = ( x, x²) Obliczamy odległość I AP I → AP = [ x , x² − 1] więc I AP I = √ x² + (x² −1)² = √ x² + x⁴ − 2 x² + 1 = √ x⁴ − x² + 1 Ta odległość będzie najmniejsza gdy g(x) = x⁴ − x² + 1 będzie miała minimum. g'(x) = 4 x³ − 2 x = 2x*( 2 x² − 1) = 2x*( √2 x − 1)*( √2x + 1) = 0 ⇔

	1		1
⇔ x = 0 lub x = −		lub x =
	√2		√2

g''(x) = 12 x² − 2

	1
g''( −		) = 4 > 0 − g osiąga minimum lokalne
	√2

	1
g''(		) = 4 > 0 − g osiąga minimum lokalne
	√2

zatem

	1		1
x = −		} lub x =
	√2		√2

	1
y =
	2

	√2		1		√2		1
P = (U{ −		,		) lub P = (		,		)
	2		2		2		2

ZKS: O ile się nie mylę to

	1		1
P = (±		;		).
	√2		2

M.: dziękuję bardzo,potrzebowalam tylko rozpoczęcia,dziękuję!

M.: Janek usunął niewymierność,to dlatego

ZKS: To ja pokażę inny sposób y = x² oraz A = (0 ; 1) |AP| = √x² + (y − 1)² = √y² − y + 1 szukamy najmniejszej odległości, a zatem musimy policzyć najmniejszą wartość tego wyrażenia. Należy policzyć wierzchołek paraboli f(y) = y² − y + 1

	1		1		1
yw =		⇒ x2 =		⇒ x = ±		.
	2		2		√2

ZKS: Kurde, a ja głupi myślałem, że to co innego (jakbyś zwróciła uwagę na to, kiedy napisałem zauważyłabyś, że to jest napisane w tym samym czasie, czyli po prostu dałem odpowiedź, a nie poprawiałem kogoś).

52: ZKS spokojnie

M.: No nie zauważyłam..

M.: Poza tym poo co mi odpowiedz,skoro nie znalabym sposobu to jest matematyczne myslenie ,a nie tylko odpowiedzi

M.: Janek ,skąd bierze się ten zapis "I AP I = √ x2 + (x2 −1)2 = √ x2 + x4 − 2 x2 + 1 = √ x4 − x2 + 1" czy jest na to jakiś wzór czy jak?

ZKS: Przepraszam poniosło mnie. Jest to najzwyczajniejszy wzór na długość odcinka.

Janek191:

magda: dziękuję