Rachunek różniczkowy Nilred: Dzień dobry, powtarzam sobie wiadomości przed sprawdzianem i napotkałem parę problemów z z zestawem powtórzeniowym.

	x3−x2−x+1
1)Oblicz granicę limx→1
	x3−3x+2

	x2(x−1)−(x−1)
Grupuję wyrazy i otrzymuje
	x(x2−1)−2(x−1)

	(x−1)(x2−1)
⇒		⇒skracamy i powinniśmy otrzymać 0, tak?
	(x−1)(x−2)(x+1)

	√2x−7−1
2) Oblicz granicę limx→4		nie wiem jak zacząć, mnożąc obie strony przez
	√X−3−1

licznik lub mianownik i tak dostane 0 w liczniku lub mianowniku. 3)Wyznacz asymptoty wykresu f(x)= √1+x²+x Nie wiem jak się za to zabrać, powinienem liczyć lim w + i − ∞? Bardzo proszę o odpowiedź i rady

Nilred: Podbijam

Janek191:

	x −1
f(x) =
	x − 2

więc

	1 − 1
lim f(x) =		= 0
	1 − 2

x→1

Nilred: czyli dobrze policzyłem 1wszy podpunkt, czy mógłbyś może pomóc mi z 2gim i trzecim?

Janek191:

	√2x −7 − 1
2) f(x) =		=
	√x − 3 − 1

	2 x − 7 − 1     √2x −7 + 1
=		=
	x − 3 − 1     √x −3 + 1

	2*( x − 4)		√ x −3 + 1
=		*		=
	√2x − 7 + 1		x − 4

	2√x −3 + 2
=
	√2 x − 7 + 1

więc

	2 √4 −3 + 2		4
lim f(x) =		=		= 2
	√2* 4 − 7 + 1		2

x→ 4

Janek191: W liczniku i mianowniku korzystamy z wzoru

	a2 − b2
a − b =
	a + b

Nilred: Bardzo dziękuję, ta metoda mi nawet do głowy nie przyszła... A czy w 3cim wiesz jak powinienem zacząć?

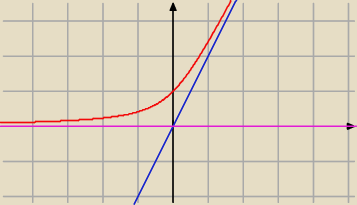
Janek191: Pozioma y = 0 Ukośna y = 2 x

Nilred: Okej, ale nie wiem jak je wyliczyłeś. Mam liczyć Limx→∞+ i limx→∞− ?

Janek191: lim f(x) = 0 i f(x) > 0 x → −∞ więc y = 0 − równanie asymptoty poziomej =================================

f(x)		1
	= 1 + √(1 +		)
x		x2

więc

	1
lim ( 1 + √(1 +		) = 2 = m
	x2

x → +∞ oraz ( f(x) − 2 x) = √1 + x² + x − 2x = √1 + x² − x więc lim ( √1 + x² − x) = 0 = k x →+∞ Równanie asymptoty ukośnej prawostronnej jest postaci y = m x + k czyli y = 2 x ======

Nilred: Bardzo dziękuję za pomoc, może mi lepiej na sprawdzianie pójdzie. Życzę spokojnego wieczoru.