Funkcja homograficzna
nicpoń: | | x+3 | |
Dany jest wzór funkcji f, f(x) = |
| |
| | x+2 | |
a) narysuj wykres funkcji f i podaj jej zbiór wartości.
b) Określ, dla jakich argumentów funkcja przyjmuje wartości nieujemne.
c) W tym samym układzie sporządź wykres funkcji g(x) = f(|x|)
d) następnie określ ilość rozwiązań równania g(x)=m w zależności od m.
20 maj 15:41
J:
1) Dziedzina
| | x+2 +1 | | 1 | |
2) f(x) = |
| = 1 + |
| .... |
| | x+2 | | x+2 | |
| | 1 | |
hiperbola |
| przesunięta o wektor v = [−2,1] |
| | x | |
20 maj 15:44
J:
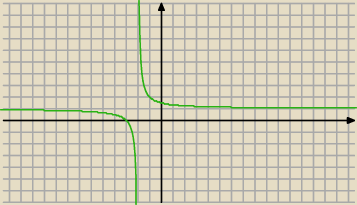
20 maj 15:45
Tysiek: Przedstaw tę postać ogólną jako postać kanoniczną funkcji homograficznej.
| | x+2+1 | | 1 | |
f(x)= |
| = |
| + 1 |
| | x+2 | | x+2 | |
Asymptoty:
x = p = −2
y = q = 1
Sporządź wykres, resztę odczytasz właśnie z wykresu

20 maj 15:49
sama.słodycz: i skąd ja mam wiedzieć że jest 2,1 czy 0 rozwiązań ?
20 maj 16:35

