nie wiem co to jest sieczna okręgu
cuusy: dla jakich wartości parametru m prosta l o równaniu y=2x+m jest sieczną do okręgu o równaniu
(x−1)2+(y+3)2=5
20 maj 10:53
5-latek: Jeśli nie wiesz to przeczytaj w książce lub na gogle
20 maj 10:54
5-latek: Jak już się dowiesz co to jest sieczna to napisz jaki jest srodek i promien tego okręgu
20 maj 10:55
J:
i poszukaj wzoru na odległość punktu od prostej

20 maj 11:01
5-latek:
No to tak
Prosta jest sieczna okręgu jeśli ma z nim 2 punkty wspólne (czyli odleglosc prostej od srodka
okręgu jest mniejsza od promienia tego okręgu
Najdluasza sieczna okręgu jest jego srednica
Prosta jest styczna do okręgu jeśli ma 1 punkt wspólny z okręgiem (czyli odleglosc prostej od
sroka okręgu jest rowna promieniowi tego okręgu
20 maj 11:31
5-latek: Wiesz kolego takie rzeczy to należy wiedzieć .
Możesz np. nie wiedzieć jak cos potem przeksztalcic ale to to musisz
20 maj 11:32
J:
... co to jest najdłuższa sieczna ?

20 maj 11:34
Benny: @
5−latku ja bym chyba tak tego nie określił. Sieczna to prosta, więc nie możemy mówić, że
jest to średnica, ponieważ średnica to odcinek o określonej długości. Ja tak myślę

20 maj 11:44
J:
i słusznie myślisz ... chciał pewnie powiedzieć,że odcinek siecznej przechodzącej przez środek
okręgu jest jego średnicą

20 maj 11:50
5-latek: I dobrze myślisz

Gdyz srednica okręgu będzie
cieciwa która przechodzi przez srodek okręgu.
Okreslenie : Cieciwa okręgu nazywamy odcinek który laczy dwa dowolne punkty okręgu
20 maj 11:57
J:
do rzeczy:
| | −2 − 3 − m | | −5 − m | | −5 − m | |
I |
| I < √5 ⇔I |
| I < √5 ⇔ −√5 < |
| < √5 |
| | √5 | | √5 | | √5 | |
20 maj 12:04
J:
⇔ − 5 < −5 − m < 5 ⇔ 0 < − m < 10 ⇔ 0 > m > − 10 ⇔ m ∊ (−10,0)
20 maj 12:06
J:
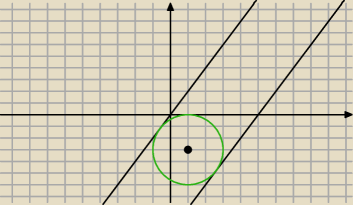
20 maj 12:14
J:
na rysunku mamy proste: y = 2x oraz y = 2x −10 ,
wszystkie proste do nich równoległe i leżące pomiedzy nimi spełniaja warunki zadania
20 maj 12:16
cuusy: dziękuje wszystkim za pomoc
21 maj 08:31
pigor: ..., dla jakich wartości parametru m prosta l o równaniu y=2x+m
jest sieczną okręgu o równaniu (x−1)
2+(y+3)
2 = 5 .
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
ano ⇔ układ równań y=2x+m i (x−1)
2+(2x+m+3)
2 = 5 ma dokładnie 2 rozwiązania,
czyli ⇔ równanie kwadratowe x
2−2x+1+4x
2+4x(m+3)+(m+3)
2 = 25 ⇔
⇔ 5x
2+(4m+12−2)x+1+(m+3)
2 = 0 ma dokładnie 2 rozwiązania, czyli ⇔
⇔ jego wyróżnik
Δm ≥ 0 ⇔ (4m+10)
2−20(1+(m+3)
2) ≥ 0 /:4 ⇔
⇔ (2m+5)
2−5−5(m+3)
2 ≥ 0 ⇔ 4m
2+20m+25−5m
2−30m−45−5 ≥ 0 ⇔
⇔
m2+10m+25 ≤ 0 ⇔ (m+5)
2 ≤ 0 ⇔ |m+5| ≤ 0 ⇔
m = −5. ...

21 maj 16:01
pigor: .. , o kurde
oczywiście "moja" Δ powinna być tylko > 0 (2 różne rozwiązania )
to po pierwsze, a ponadto musiałem kopnąć się gdzieś w rachunkach
przepraszam ...
21 maj 16:12

 No to tak
Prosta jest sieczna okręgu jeśli ma z nim 2 punkty wspólne (czyli odleglosc prostej od srodka
okręgu jest mniejsza od promienia tego okręgu
Najdluasza sieczna okręgu jest jego srednica
Prosta jest styczna do okręgu jeśli ma 1 punkt wspólny z okręgiem (czyli odleglosc prostej od
sroka okręgu jest rowna promieniowi tego okręgu
No to tak
Prosta jest sieczna okręgu jeśli ma z nim 2 punkty wspólne (czyli odleglosc prostej od srodka
okręgu jest mniejsza od promienia tego okręgu
Najdluasza sieczna okręgu jest jego srednica
Prosta jest styczna do okręgu jeśli ma 1 punkt wspólny z okręgiem (czyli odleglosc prostej od
sroka okręgu jest rowna promieniowi tego okręgu



 Gdyz srednica okręgu będzie cieciwa która przechodzi przez srodek okręgu.
Okreslenie : Cieciwa okręgu nazywamy odcinek który laczy dwa dowolne punkty okręgu
Gdyz srednica okręgu będzie cieciwa która przechodzi przez srodek okręgu.
Okreslenie : Cieciwa okręgu nazywamy odcinek który laczy dwa dowolne punkty okręgu

