p
Radek:
Hey, potrzebuje pomocy z kilkoma zadaniami

1. Rzucamy dwa razy kostką. Jakie jest prawdopodobieństwo otrzymania za każdym razem
innej liczby oczek? To samo pytanie dla trzech rzutów kostką.
2. Mamy cztery karty: dwie czerwone i dwie czarne. Wyciągamy losowo (bez zwracania)
dwie. Co jest bardziej prawdopodobne: to, że obie będą w tym samym kolorze, czy to, że będą
w różnych kolorach?
Z góry dziękuję za pomoc

19 maj 23:37
Benny: 1. za pierwszym razem mamy 6 możliwości wyrzucenia jakiejś liczby oczek, a za drugim już 5,
ponieważ liczba oczek nie może się powtarzać. Analogicznie dla 3 rzutów.
Dla 2:
|Ω|=36
|A|=30
Dla 3:
|Ω|=216
B=120
19 maj 23:42
Radek:
2 ?
19 maj 23:56
Radek: ?
20 maj 00:07
Radek: jakas podpowiedz ?
20 maj 00:14
Draghan:
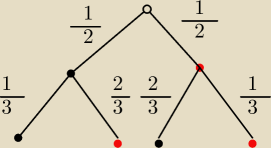
A − ten sam kolor.
| | 1 | | 1 | | 1 | | 1 | |
P(A) = |
| * |
| + |
| * |
| |
| | 2 | | 3 | | 2 | | 3 | |
B − różne kolory
| | 1 | | 2 | | 1 | | 2 | |
P(B) = |
| * |
| + |
| * |
| |
| | 2 | | 3 | | 2 | | 3 | |
20 maj 00:17
Radek:
Dziękuję Panowie
20 maj 00:21
Radek:
Coś nie tak bo P(B) wyszło bardziej prawdopodobne niż P(A) a w odpowiedzi jest inaczej
20 maj 00:26
Radek: ?
20 maj 00:28
Draghan: Ja nie widzę błędu. Może to przez późną porę...

Analiza lewej części drzewka:
1. Wyciągam czarną kartę. Szansa na to jest 1/2. Zostaje jedna czarna i 2 czerwone.
2. Następnie wyciągam:
a) znów czarną kartę, szansa na to jest 1/3, bo jest tylko 1 czarna karta na trzy,
b) czerwoną kartę, szansa 2/3 − dwie czerwone karty na trzy.
Analogicznie prawa część drzewka.
Jednakowy kolor: trzeba zsumować gałęzie z jednakowym kolorem: 1/2*1/3 + 1/2*1/3...
Różne kolory: 1/2*2/3 + 1/2*2/3... Naprawdę wygląda ok...

20 maj 00:44
Radek: ale wyszło, że P(B) jest bardziej prawdodpodbne od P(A)
20 maj 00:48
Bogdan:
P(B) = P(A') = 1 − P(A)
20 maj 00:49
Radek:
Panie Bogdanie P(A) jest prawidłowo policzone ?
20 maj 00:50
Draghan: Ja również bym prosił o podpowiedź, bo nie daje mi to spokoju...

20 maj 01:00
Radek: /
20 maj 01:05
Bogdan:
Prawidłowo
20 maj 01:06
Radek:
Dziękuję. Dobranoc
20 maj 01:08
Draghan: Dziękuję. Obawiałem się, że może zapomniałem, jak się korzysta z "drzewka"...

Teraz mogę iść
spać.

Dobranoc.

20 maj 01:08
Bogdan:
Proszę spróbować rozwiązać zadanie bez drzewka
20 maj 01:10
Bogdan:
i dobranoc

20 maj 01:10
Draghan: Szczerze mówiąc, to padam.

Ale spróbuję. I dziwne rrzeczy mi wychodzą. Teraz jeszcze bardziej proszę o poprawienie mnie.
Zdarzenie elementarne to wylosowanie
zbioru dwóch kart (kolejność nieważna).
Ω = {(
C C), (
C C), (
C C)}
|Ω| = 3
A − zdarzenie pol. na wylosowaniu dwóch kart jednego koloru
A = {(
C C), (
C C)}
|A| = 2
B − zdarzenie, pol. na wylosowaniu dwóch różnych kart:
B = {(
C C)}
|B| = 1
| | 1 | |
P(B) = |
| ... Zupełnie odwrotnie, niż poprzednio...?  |
| | 3 | |
20 maj 01:24
PW: Fatalne oznaczenia stosujesz. Co ma oznaczać {C C}? Jak coś takiego widzę, to wpadam w irytację
− gdyby elementami zbiorów były liczby, to napisałbyś np. {11}?
Mamy zbiór K = {c
1, c
2, b
1, b
2}. Tworzymy wszystkie możliwe dwuelementowe podzbiory tego
zbioru:
Ω = { {c
1, c
2}, {b
1, b
2}, {c
1, b
1}, {c
1, b
2}, c
2, b
1}, {c
2, b
2} }.
Zdarzeń elementarnych jest raptem 6, można było je wypisać. Kto lubi wzory, policzy
Dla rozwiązania zadania nawet nie trzeba było tego liczyć. wystarczyło napisać:
Zdarzenie A − wylosowano karty tego samego koloru
A = { {c
1, c
2}, {b
1, b
2} },
a więc |A| = 2.
Zdarzenie B − "wylosowano karty różnych kolorów (jedną czerwoną, drugą czarną)"
B = A',
a więc |B| = 6 − 2 = 4 (kto nie liczył |Ω|, po prostu wypisze B i policzy palcem, że |B| = 4) .
Ponieważ |B| > |A|, na mocy klasycznej definicji prawdopodobieństwa
P(B) > P(A).
Prawdopodobieństw nie musieliśmy liczyć, są one proporcjonalne do liczby zdarzeń sprzyjających
(większa liczba zdarzeń sprzyjających − większe prawdopodobieństwo).
A stosowanie drzewka do takiego zadania jest bez sensu, co słusznie
Bogdan z właściwą
sobie delikatnością zasugerował.
20 maj 13:39
Draghan: Późno już było, dlatego nie bawiłem się w finezyjne opisywanie i oznaczenia.
Tak na marginesie − tam nie ma {CC}, tylko { (C C) } − nie irytuj się, PW, bo ja
to akurat marny ku temu powód. Kolory są równie dobrym sposobem na rozróżnienie elementów, co
liczby. Chyba że ktoś ma problem z ich prawidłowym odbiorem.
Proszę, wyjaśnij dlaczego jest bez sensu − poza tym, że daje błędny wynik, co jest oczywiste.
20 maj 16:11
Radek:
Mógłbym prosić o rozpisanie 1 b mi wychodzi 11/30
20 maj 16:31
52: 1b)
|Ω| = 63
X X X
6 5 4
W pierwszym rzucie mogą pojawić się wszystkie cyfry, zatem 6
W drugim rzucie mogą pojawić się wszystkie cyfry oprócz tej co była w pierwszym rzucie, zatem 5
W trzecim rzucie mogą pojawić się wszystkie cyfry oprócz tej co była w pierwszym rzucie i
drugim rzucie, zatem 4
|B|=6*5*4
20 maj 17:21
52: Draghan jaką ty dałeś |Ω| ? Dałeś 3 co już jest bez sensu.
Masz 4 karty losujesz dwie(na raz) bez zwracania. To ile mam możliwości ?
Zresztą
PW jak zawsze pięknie ci to opisał zarówno matematycznie i jak tak żeby zrozumieć

20 maj 17:24
PW: Nie ma sensu rysowanie drzewka, gdy liczymy prawdopodobieństwo za pomocą "klasycznej definicji
prawdopodobieństwa". Mamy ustalić ile jest wszystkich zdarzeń, ile zdarzeń sprzyja zdarzeniu A
i podzielić te dwie liczby przez siebie − co tu rysować?
Drzewko jest dobrą ilustracją dla losowania dwuetapowego. Na przykład − w pierwszym etapie
losujemy urnę za pomocą rzutu kostką, umawiamy się, że jeśli wypadnie mniej niż 5, to w drugim
etapie wyciągamy kulę z urny nr 1. Jeśli wypadnie 5 lub 6 − będziemy losować z urny nr 2.
W urnach są kule czerwone i białe. W pierwszej jest 5 czerwonych i 1 biała, w drugiej − 2
czerwone i 3 białe.
Są więc
dane prawdopodobieństwa (zaszyfrowane w treści zadania w postaci łatwych zadanek
rozwiązywanych w pamięci):
| | 4 | | 2 | | 5 | | 2 | |
P(U1) = |
| , P(U2) = |
| , P(C|U1) = |
| , P(C|U2) = |
| . |
| | 6 | | 6 | | 6 | | 5 | |
Tutaj jest sens rysować drzewko, które dobrze oddaje wzór na prawdopodobieństwo całkowite (wzór
Bayesa).
Zazwyczaj nie wypisuje się ani zbioru Ω, ani zbioru C − "wylosowano kulę czerwoną". W tym
wypadku nie warto, bo nie działa twierdzenie zwane klasyczną definicją prawdopodobieństwa
(wyciągnięcie kuli czerwonej z urny nr 1 ma inne prawdopodobieństwo niż wyciągnięcie kuli
czerwonej z urny nr 2), a więc liczenie "na sztuki" nie da poprawnego wyniku.
Irytacja moja nie miała charakteru personalnego. Widzę powszechną tendencję do niedbałego
formułowania problemu, co przynosi często fatalne skutki, bo dąży się do wyniku − "ile to
jest", zamiast najpierw zdać sobie sprawę "co ja właściwie będę liczyć". Ty jesteś już wyżej,
pewne rzeczy można sobie darować na zasadzie, że proste rzeczy wszyscy wiedzą, ale w
początkowej fazie nauki to powinno być podstawą − określić jasno co liczę i jakie twierdzenia
stosuję w tym celu.
Dlatego jestem w ogóle wrogiem "drzewek", bo uczą rysowania gałązek (czasem nawet uda się
uzyskać dobry wynik komuś, kto zupełnie nie rozumie co liczy).
20 maj 17:54
Radek:
Jakie jest prawdopodobieństwo tego, że w grupie 3 losowo wybranych osób NIE MA
takich dwóch osób, które obchodzą urodziny w tym samym dniu? Zakładamy dla uproszczenia,
że każdy rok ma 365 dni.
b) To samo pytanie dla 20 osób. c)* Ile osób powinno być w grupie, aby to prawdopodobieństwo
było równe mniej więcej 1/2?
20 maj 20:11
PW: Wbrew pozorom (losowy wybór trzech osób) zdarzeniami elementarnymi nie są trzyelementowe
zbiory.
Wynikiem doświadczenia są trzy informacje: dzień narodzin pierwszej osoby (jedna liczb ze
zbioru D = {1, 2, 3, ..., 365}), dzień narodzin drugiej osoby, dzień narodzin trzeciej osoby.
Zdarzeniem elementarnym jest więc każdy ciąg
(x1, x2, x3),
którego wyrazy należą do zbioru D.
Jak wiadomo ciągów takich jest 3653,
|Ω| = 3653.
Może niepotrzebnie to piszę, ale w tym doświadczeniu losowość polega na tym, że mając trzy
nieznane nam osoby nie wiemy kiedy się rodziły, a więc ich dni narodzin są dla nas
wielkościami losowymi − mogą być zupełnie dowolnymi liczbami (także jednakowymi) ze zbioru D.
Każdy ciąg różnowartościowy, jak np. (301, 45, 200) jest zdarzeniem sprzyjającym zdarzeniu
A − "każda z trzech badanych osób urodziła się w innym dniu roku".
Jak wiadomo różnowartościowych 3−wyrazowych ciągów o wartościach w D jest ...
20 maj 20:31
Radek:
@PW chodzi mi dokładniej o podpunkt c ) ?
| | 356*364*363 | |
a) P(A)= |
| |
| | 3652 | |
| | 365*364*363*.....346 | |
b) P(A)= |
| ? |
| | 36519 | |
20 maj 20:49
Radek: ?
20 maj 21:19
PW: Poddaję się. Ani dla a), ani dla b) nie podałeś poprawnych odpowiedzi.
20 maj 21:25
Draghan: Dziękuję za odpowiedź.

20 maj 21:41
 1. Rzucamy dwa razy kostką. Jakie jest prawdopodobieństwo otrzymania za każdym razem
innej liczby oczek? To samo pytanie dla trzech rzutów kostką.
2. Mamy cztery karty: dwie czerwone i dwie czarne. Wyciągamy losowo (bez zwracania)
dwie. Co jest bardziej prawdopodobne: to, że obie będą w tym samym kolorze, czy to, że będą
w różnych kolorach?
Z góry dziękuję za pomoc
1. Rzucamy dwa razy kostką. Jakie jest prawdopodobieństwo otrzymania za każdym razem
innej liczby oczek? To samo pytanie dla trzech rzutów kostką.
2. Mamy cztery karty: dwie czerwone i dwie czarne. Wyciągamy losowo (bez zwracania)
dwie. Co jest bardziej prawdopodobne: to, że obie będą w tym samym kolorze, czy to, że będą
w różnych kolorach?
Z góry dziękuję za pomoc 
 A − ten sam kolor.
A − ten sam kolor.
 Analiza lewej części drzewka:
1. Wyciągam czarną kartę. Szansa na to jest 1/2. Zostaje jedna czarna i 2 czerwone.
2. Następnie wyciągam:
a) znów czarną kartę, szansa na to jest 1/3, bo jest tylko 1 czarna karta na trzy,
b) czerwoną kartę, szansa 2/3 − dwie czerwone karty na trzy.
Analogicznie prawa część drzewka.
Jednakowy kolor: trzeba zsumować gałęzie z jednakowym kolorem: 1/2*1/3 + 1/2*1/3...
Różne kolory: 1/2*2/3 + 1/2*2/3... Naprawdę wygląda ok...
Analiza lewej części drzewka:
1. Wyciągam czarną kartę. Szansa na to jest 1/2. Zostaje jedna czarna i 2 czerwone.
2. Następnie wyciągam:
a) znów czarną kartę, szansa na to jest 1/3, bo jest tylko 1 czarna karta na trzy,
b) czerwoną kartę, szansa 2/3 − dwie czerwone karty na trzy.
Analogicznie prawa część drzewka.
Jednakowy kolor: trzeba zsumować gałęzie z jednakowym kolorem: 1/2*1/3 + 1/2*1/3...
Różne kolory: 1/2*2/3 + 1/2*2/3... Naprawdę wygląda ok... 

 Teraz mogę iść
spać.
Teraz mogę iść
spać.  Dobranoc.
Dobranoc. 

 Ale spróbuję. I dziwne rrzeczy mi wychodzą. Teraz jeszcze bardziej proszę o poprawienie mnie.
Zdarzenie elementarne to wylosowanie zbioru dwóch kart (kolejność nieważna).
Ω = {(C C), (C C), (C C)}
|Ω| = 3
A − zdarzenie pol. na wylosowaniu dwóch kart jednego koloru
A = {(C C), (C C)}
|A| = 2
B − zdarzenie, pol. na wylosowaniu dwóch różnych kart:
B = {(C C)}
|B| = 1
Ale spróbuję. I dziwne rrzeczy mi wychodzą. Teraz jeszcze bardziej proszę o poprawienie mnie.
Zdarzenie elementarne to wylosowanie zbioru dwóch kart (kolejność nieważna).
Ω = {(C C), (C C), (C C)}
|Ω| = 3
A − zdarzenie pol. na wylosowaniu dwóch kart jednego koloru
A = {(C C), (C C)}
|A| = 2
B − zdarzenie, pol. na wylosowaniu dwóch różnych kart:
B = {(C C)}
|B| = 1


