Ekstrema funkcji.
MAJA: Witam, mam problem ze zrozumieniem nastepujacego typu przykladu dotyczacego obliczania
ekstremow lokalnych funkcji:
y=|x
2+x−2|
Oto moje czesciowe rozwiazanie:
zaczelam od wyznaczenia dziedziny :
Df=R
nastepnie od rozpisania funkcji, korzystajac z definicji wartosci bezwzglednej:
f(x)= 1.x
2+x−2 , gdzie x∊ (−∞,−2) U (1,∞)
2.−x
2−x+2, gdzie x∊(−2,1)
obliczam pochodne:
f`(x)=1.2x+1
2.−2x−1
f`(x)=O ⇔x>−1/2,
f`(x)>O⇔ x∊(−1/2,∞)
f`(x)<O⇔x∊(−∞,−1/2)
f(−1/2)=9/4 − maksimum lokalne
Tak naprawde to nie wiem co mam zrobic z:
f(x)= 1.x
2+x−2 , gdzie x∊ (−∞,−2) U (1,∞)
2.−x
2−x+2, gdzie x∊(−2,1)
Nie jestem pewna czy takowy zapis jest poprawny i ogolnie nie rozumiem, w jaki sposob wyznaczyc
ekstremum z wartosci bezwzglednej. Dodam, ze poza wyliczonym przeze mnie maksimum lokalnym
powinno byc takze minimum lokalne f(1)=0 oraz f(−2)=O.Cazy moglabym prosic o pomoc w
wyznaczeniu tych ekstremow i wytlumaczeniu zagadnienia?Dziekuje slicznie za odpowiedz
Rudy:
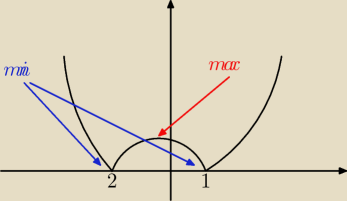
Definicja ekstremum lokalnego mówi że w otoczeniu funkcja nie przyjmuje wartości
większych/mniejszych. Z wykresu widać że poza maksimum są dwa miejsca gdzie funkcja w
otoczeniu przyjmuje wartości najmniejsze. Problem polega na tym że w tych punktach funkcja nie
jest różniczkowalna, zatem nie ma pochodnej, czyli ta pochodna nie może być równa 0 (bo jej
nie ma). Te punkty to jednak minima. Możesz po prostu wyznaczyć ich wartości podstawiając
argumenty −2 i 1 do wzoru.
MAJA: Czy ten zapis jest poprawny?
f(x)= 1.x2+x−2 , gdzie x∊ (−∞,−2) U (1,∞)
2.−x2−x+2, gdzie x∊(−2,1)
Na matematyce musimy wszystko robic po kolei, czy moglby mi pan napisac po kolei etapy dzieki
ktorym moglabym dojsc do uzyskania akurat argumentow −2 i 1 a nie innych?Dziekuje z gory
slicznie
