Graniastosłupy. Zadanie związane z trygonometrią rozwiązanie.
Ravana:
Zadanie 1
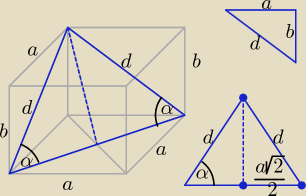
W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość d i tworzy z
przekątną podstawy poprowadzoną z tego samego wierzchołka kąt o mierze α. Wyznacz objętość
graniastosłupa.
Rozwiązanie.
Na rysunku zielonym kolorem zaznaczyłam kąty proste, a na czerwono− kąt α.
Dane: d, α Szukane: V= ?
| | e2 | | e | |
cosα= |
| d* cosα= |
| |*2 e= 2*d*cosα |
| | d | | 2 | |
a
2 + a
2=e
2
2a
2= (2*cosα*d)
2
2a
2= 4* cos
2α*d
2 |:2
a
2= 2* cos
2α*d
2
a=
√2*cosα*d
d
2= H
2 + a
2
H
2= d
2 − a
2
H
2= d
2− (
√2*cosα*d)
2
H
2= d
2−2*cos
2α*d
H=
√d2−2*cos2α*d2
H=
√d2*(1− 2*cos2α)
H= d*
√1−2*cos2α
V= (
√2*cosα*d)
2*d*
√1−2*cos2α
V= 2*cos
2α*d
2*d*
√1−2*cos2α
V= 2*d
3*cos
2α*
√1−2*cos2α [j
3]
Takie zadania przerażają lekko. Dziś miała sprawdzian i mogę stwierdzi, że ja matematyki nie
umiem. Może komuś się ono przyda jako wzorzec do lepszych obliczeń. ja rozkminiłam to zadanie
oczywiście po sprawdzianie...
Zdajmy z matmy!

i maturę z niej też
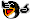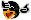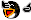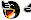
 Zadanie 1
W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość d i tworzy z
przekątną podstawy poprowadzoną z tego samego wierzchołka kąt o mierze α. Wyznacz objętość
graniastosłupa.
Rozwiązanie.
Na rysunku zielonym kolorem zaznaczyłam kąty proste, a na czerwono− kąt α.
Dane: d, α Szukane: V= ?
Zadanie 1
W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość d i tworzy z
przekątną podstawy poprowadzoną z tego samego wierzchołka kąt o mierze α. Wyznacz objętość
graniastosłupa.
Rozwiązanie.
Na rysunku zielonym kolorem zaznaczyłam kąty proste, a na czerwono− kąt α.
Dane: d, α Szukane: V= ?
 i maturę z niej też
i maturę z niej też