Udowodnij, że pole trójkąta ostrokątnego jest równe iloczynowi połowy obwodu i d Dumdum: Udowodnij, że pole trójkąta ostrokątnego jest równe iloczynowi połowy obwodu i długości promienia okręgu wpisanego w ten trójkąt. Pomógłby ktoś? Jak na razie mam wypisane (a+b+c)/2 * r = 1/2*a*h i wszystko oznaczone na rysunku.

PW: Trzeba zobaczyć trzy trójkąty o podstawach a, b, c i wierzchołkach w S (S − środek okręgu wpisanego).

Ajtek: Pole dużego Δ to suma trzech pól małych Δ i wysokości r.

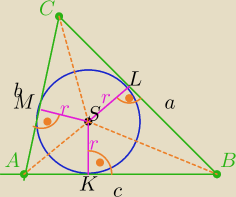
Mila: Promien okręgu wpisanego w trójkąt jest prostopadły do boku trójkąta w punkcie styczności.

	1		1		1
PΔABC=		*c*r+		*a*r+		*b*r=
	2		2		2

	1
=		*r*(c+a+b)⇔
	2

	a+b+c
PΔABC=		*r
	2

cnw

Dumdum: Ooo, dziękuje bardzo. Teraz to zrozumiałem

Mila: