Wykaż że ciąg (an) jest ciągiem malejącym jeśli: Łukasz: an= − 0,1n+20

Przemysław: a_n+1−a_n=?

Łukasz: a nie czasami muszę an+1 obliczyć?

Łukasz: na początek

Łukasz: ?

Łukasz: ?

52: Możesz, nie musisz

Łukasz: an+1−an= −0,1(n+1)+20−(−0,1)= tak to ma być?

52: −0,1(n+1)+20−(−0,1n+20)=...

Łukasz: mnoże to i pózniej redukcja?

52:

Łukasz: wynik to −0,1?

Łukasz: 2.Naszkicuj wykres ciągu (an) jeśli dany jest wyraz ogólny tego ciągu: an= −n+7,nEN

Łukasz: proszę o pomoc

52: To no szkicuj wstawiaj za n kolejno 1,2,3,4,5...

Łukasz: 52 a wynik z godz 19:36 ok?

52:

Łukasz: więc... n=−1+7=6 an2=5 an3=4 3 2 1 0 w tabelce było tam gdzie y to an a gdzie x n wtedy wychodzą takie punkty

Łukasz: nie umiem rysować takiej tabelki

Łukasz: 52 jak myślisz ok jest?

52: Myślę, że tak, musisz to narysować

Łukasz: Dany jest wyraz ogólny nieskończonego ciągu (an) Napisz cztery początkowe wyrazy tego ciągu Następnie oblicz a2k,a3k,a2k−1 oraz a5k+3 gdzie k E N an=2n²−4n+1,nEN

Łukasz: ?

Łukasz: ?

Łukasz: proszę o pomoc

t: a_n = 2n² − 4n + 1, n ∊ N Cztery początkowe: {a₁, a₂, a₃, a₄}, a₁ = 2 * (1)² − 4 * 1 + 1 = 2 − 4 + 1 = −1 a₂ = ... (Twoja działka) a₃ = ... a₄ = ... Druga część: a_2k, a_3k, a_{2k − 1}, a_{5k + 3} a_2k = 2 * (2k)² − 4 * 2k + 1 = 8k² − 8k + 1 Resztę robisz analogicznie.

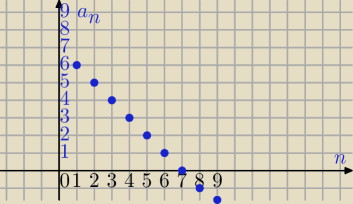
Mila: 2.Naszkicuj wykres ciągu (an) jeśli dany jest wyraz ogólny tego ciągu: a_n= −n+7,n∊N a₁=−1+7=6 a₂=−2+7=5 a₃=−3+7=4 a₄=−4+7=3 a₅=−5+7=2 a₆=−6+7=1 a₇=−7+7=0 a₈=−8+7=−1 a₉=−9+7=−2

Łukasz: zaraz wszystko będzie Mila jak zawsze piękny wykres

Łukasz: czyli za a2 podstawiam 2 za a3 3 i za a4 4 wyniki: a2=5 a3=15 a4=29

Łukasz: a3k=12k−12k+1

Łukasz: dobrze to?

Łukasz: ?

Mila: a_n = 2n² − 4n + 1, n ∊ N a_3k=2*(3k)²−4*(3k)+1 a_3k=2*9k²−12k+1=18k²−12k+1 a_2k−1 ma być czy a_2k−1 ? Zobacz z lewej strony pola tekstowego jak to się pisze.

Łukasz: a2k−1 nie wiem jak to może ktoś wyliczyć

Łukasz: ?

Łukasz: które wyrazy ciągu an są dodatnie jeśli: an=2n−7,nEN

Łukasz: ?

Łukasz: proszę o pomoc

Mila: Łukasz widzę, że nie starasz się zrozumieć.Będziesz miał kłopoty. a_n = 2n² − 4n + 1, n ∊ N a_2k−1=2*(2k−1)²−4*(2k−1)+1 Teraz licz , sprawdzę za chwilę.

Łukasz: przepraszam wiem jak to liczyć ale niepokoi mnie wynik 8k−4−8k−4+1

Mila: a_2k−1=2*(2k−1)²−4*(2k−1)+1= korzystamy z wzoru skróconego mnożenia (a−b)²=a²−2a*b+b² =2*(4k²−4k+1)−8k+4+1=8k²−8k+2−8k+5=8k²−16k+7