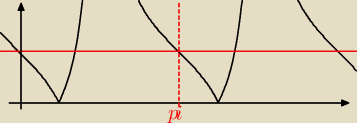
Trygonometria, zadanie z parametrem Kamila: Wyznacz wartości parametru m, m∊R, dla których równanie |tgx−1|=m²−6m ma dwa rozwiązania w przedziale <0,π>. Dla mnie warunki muszą być takie: m²−6m>0 i m²−6m≠1 z tego mamy odp. m∊(−∞;0)∪(6;+∞)\{3−√10,3+√10}. W książce w odpowiedziach jest: (3−√10;0)∪(6;3+√10) to tak jakby postawili warunki, że m²−6m>0 i m²−6m<1. Ale z wykresu widać, że powyżej 1 także mamy dwa rozwiązania. To w książce jest błąd czy czegoś nie zauważam?

J: zrób w miarę porządny szkic i zobaszysz,że powyżej prostej: y = 1 są trzy rozwiązania

J: a nawet teraz zauważyłem,że widać to na Twoim wykresie ... popatrz powyżej czerwonej prostej .prosta przetnie wykres w trzech punktach

J: nie tak .... źle popatrzyłem na przedział ... trzy rozwiązania będą dla y = 1

Kamila: No właśnie trzy rozwiązania będą dla y=1, więc jedynkę wykluczam, a powyżej? Ja chyba jestem jakaś ślepa, bo widzę dwa rozwiązania...

J: OK .. powyżej jedynki są nadal dwa rozwiązania .. .zatem wykluczamy tylko y = 1