MaRek: W trójkącie ostrokątnym ABC poprowadzono wysokość CD. Punkt E należy do boku AC, a odcinek BE i CD przecinają się w punkcie H, przy czym wiadomo, że CD = DB i HD = DA. Wykaż, że odcinek BE jest wysokością trójkąta ABC.

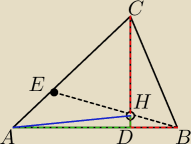
vaultboy: <BDC=90 ΔDBH≈ΔDCH bo DH/AD=DB/DC i <ADC=<HDB zatem z podobieństwa tych trójkątów dostaję <HCE=<HBD=<EBD zatem z twierdzenia o kącie wpisanym dostajemy, że punkty DBCE leżą na jednym okręgu Zatem 90=<BDC=<BEC a to daje tezę

Kulok: Dzieki