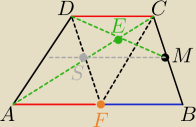MaXior: Dany jest trapez ABCD o podstawach AB i CD, że AB = 2* CD. Punkt M jest środkiem ramienia BC. Odcinki DM i AC przecinają się w punkcie E. Oblicz AE / EC

MaXior: pomoze ktos? 😪😪

vaultboy: Niech F będzie środkiem AB. wtedy AF=CD i AF||CD zatem AFCD jest równoległobokiem. Niech S będzie punktem przecięcia AC i DF. Skoro jest to równoległobok to S jest środkiem przekątnych. Prosta równoległa do AB przechodząca przez M będzie przecinać S (Dowód: Niech prosta równoległa do AB przechodząca przez M przecina AC w S' Z Talesa CS'/S'A=CM/MB, natomiast CM/MB=1 zatem CS'=S'A zatem S' jest środkiem AC c.k.d) Analogicznie FBCD jest równoległobokiem Stąd SMCD jest równoległobokiem (bo SM=FB=CD i SM || BF || CD) Czyli punkt E jest środkiem przekątnych SC i MD Łącząc to wszystko dostajemy AS=SC SE=EC

	AS+SE		SC+SE		3EC
czyli AE/EC=		=		=		=3
	EC		EC		EC

Eta:

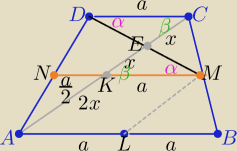
	3
|AB|=2a , |DC|=a to |NM|=		a
	2

	a
|NK|=		, |KM|=a
	2

Trójkąty KME i DEC są przystające z cechy (k,b,k) oraz trójkąty ANK i ACD są podobne w skali k=2 ⇒ |AK|=KC|=2x

	|AE|		3x
to		=		=3
	|EC|		x

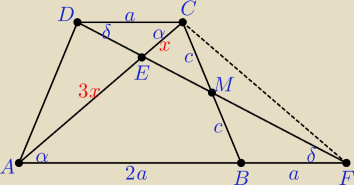Bogdan: Trójkąty BFM i MCD są przystające.

	|AE|
Trójkąty AFE i CDE są podobne w skali 3:1, stąd		= 3
	|EC|

Bogdan:

Eta:

vaultboy:

Eta:

MaXior: Dziekuje, bardzo pomogło