... ...: przekrojem osiowym stożka jest trójkąt równoboczny o boku 6 cm. oblicz objetość stożka. przyjmij π ≈ 3.

Ajtek: I w czym problem?

...: nie umiem obliczyć.. jak można to wytłumaczyć na przyszłość z góry bardzo dziękuje. przyda sie

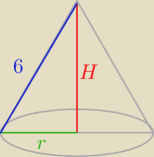
Ajtek: Przekrojem tego stożka jest Δ równoboczny. Aby obliczyć objętość, potrzebna będzie wysokość tego stożka (wysokość Δ) oraz promień podstawy, który jest równy?

...: r ?

Ajtek: r − promień podstawy tego stożka, ile jest równy? Wrócę za 15 minut.

...: 3?

nata: bardzo dobrze teraz policz H z twierdzenia Pitagorasa

...: ja matematyki w ogóle nie mogę załapać... czasem uda się coś zrozumieć ale to czasem.. dziękuje że pomagasz

t: Po co tw. Pitagorasa? Skoro to jest trójkąt równoboczny to wzór na wysokość znamy

t:

	1
Dane: a = 6, r =		* a ⇒ r = 3
	2

	a√3		6√3
h =		⇒ h =		= 3√3
	2		2

	1
Wzór na objętość: V =		* πr2 * H
	3

	1
V =		* π * 9 * 3√3 = 9√3π
	3

...: i co to już rozwiązanie ? nie chyba nie ? jezu ja nie ogarniam..

nata: Wzór znamy, ale niekoniecznie wszyscy W tablicach dostępnych na maturze, tego wzoru nie ma, a więc dobrze żeby nauczyć się, samemu sobie obliczyć

t: jeszcze podstawić za π = 3, ale widać, że liczysz na maksymalnego gotowca czyli ostateczna odpowiedź to: V = 9√3π = 27√3 [cm³]

nata: a wiesz co to jest twierdzenie Pitagorasa ?

t: To nie trzeba z Pitagorasa, więc pożytku będzie z zastosowania trygonometrii (jako, że jest to trójkąt równoboczny, to każdy kąt ma po 60^o) <− informacja dla ....

...: no nie nie liczyłam na to szczerze. muszę kartkówkę poprawić akurat to pytanie było i też chce to ogarnąć bo ja z matmy kiepska

t: to, że kiepska to nie znaczy, że nie trzeba odpowiednio wcześnie siąść nad tym i się tym zająć (tak jak w przypadku każdego innego przedmiotu z którym mamy problemy, ale to jest problem obecnej młodzieży)

nata: Czy to co napisał t jest dla ciebie jasne ?

...: obecnej młodzieży nie chce się uczyć tylko balanga. ja np chce i chciałabym to zrozumieć.. dla niektórych to zadanie było banalne dla mnie niestety nie i do tej pory nie wiem o co w nich chodzi a cały czas czytam to...

t: bo nie da się nauczyć matematyki zaczynając od całek (metafora), jeżeli chcesz zrozumieć zagadnienie zacznij od podstaw, trójkąt równoboczny, potem co to jest przekrój, co to jest stożek jak się go tworzy i to wszystko, nic innego tam nie ma

Mila: nata przecież te podstawowe wzory tłucze się od podstawówki.

nata: Ok, Ajtek zrobił ci super rysunek. Napisz czy potrafisz obliczyć tą wysokość, albo jak pisałam wcześnie z Pitagorasa, albo jak sugerował t z sinusa kąta 60⁰

...: poczekaj chwilke

...: p= a*h przez 2 p= 6*3 przez 2 p = 9 ?

...: a= 6 b= 3 c= ? c2= 6/2 + 3/2 c2= 36 + 9 c2= 45 4,5 ?

nata: c²=36−9 c²=27 c=√27 c=√9*3 c=3√3

nata: H i r są przyprostokątnymi, a 6 jest przeciwprostokątną

nata: Tej wysokości nie policzysz ze wzoru na pole, bo nie znasz tego pola

...: aha

nata: rozumiesz to co napisałam ?

...: przyprostokątnymi że są przy sobie a przeciwprostokątna że są po przeciwnych tak ?

nata: przyprostokątne, to te co są przy kącie prostym, a przeciwprostokątna − naprzeciw tego kąta.

nata: stąd zgodnie z tw. Pitagorasa 6²=3²+H² 36=9+H² H²=36 − 9 H²=27

...: ok teraz wiem

nata: i H=3√3

nata: to masz już wszystkie dane żeby podstawić do wzoru na objętość

nata: i jak wyszło ?

...: t zrobił ale możesz dać mi podobne zadanie i spróbuje zrobić obliczyć to z sinusa i podstawiać już chyba łapie to

...: pitagorasa*

nata: to przyjmij że bok trójkąta jest równy 4 cm i przeprowadź obliczenia

...: c2 = a/2 + b/2 4/2 = 3/2 + h2 h2= 16 − 9 h2 = 7 h = 3,5√3 wzór na objętość V= 1/3 * πr2 * h v= 1/3 * π* 9* 3,5√3 * 12,25√3π

nata: no jak tam obliczenia ?

...: tak ma być ?

nata: no tak, tylko że jak bok jest równy 4, to jego połowa będzie 2, czyli r=2 a nie 3 popraw to

...: c2 = a/2 + b/2 4/2 = 3/2 + h2 h2= 16 − 9 h2 = 7 h = 3,5√2 wzór na objętość V= 1/3 * πr2 * h v= 1/3 * π* 9* 3,5√2 * 12,25√2π

nata: i jeszcze jedno, jeśli h²=7 to h=√7 , ponieważ z 7 nie da się wyciągnąć pierwiastka

nata: czekam na poprawioną wersję

...: c2 = a/2 + b/2 4/2= 2/2 + h2 h2= 16 − 4 h2 = 12 h= 6√2 wzró na objętość V= 1/3 * πr2 * h V= 1/3 * π* 4* 6√2 * 36√2π

...: dobrze ?

nata: h²=12 h²=4*3 h=√4*3 h=2√3 i teraz należy podstawić do wzoru. Źle wyciągasz pierwiastek, zobacz jak ja to zrobiłam.

nata: jest to dla ciebie zrozumiałe?

...: tak jutro będę jeszcze powtarzać ćwiczyć dziękuje a teraz mykam jutro wbije tu można poćwiczyć i zobaczyć co pamiętam i mam jeszcze inne zadania też do pomocy zrozumienia

nata: ok, ja też już spadam spać