wyznacz zbiór wartości funkcji yano:

	x2+1
Wykaż że zbiorem wartości funkcji f(x)=		jest przedział R−<−2;2>
	x

Jestem w pierwszej klasie LO

Janek191:

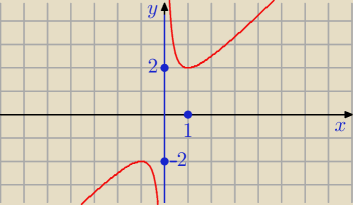
	x2 + 1		1
f(x) =		= x +		, x ≠ 0
	x		x

Dla x > 0 prawdziwa jest nierówność

	1
( √x −		)2 ≥ 0
	√x

	1		1
x − 2*√x*		+		≥ 0
	√x		x

	1
x +		≥ 2
	x

zatem f(x) ≥ 2 dla x > 0

	1		1
Funkcja f jest nieparzysta, bo f(− x) = − x +		= − (x +		)
	−x		x

więc dla x < 0 jest f(x) ≤ − 2 ckd.

b.: W zasadzie ten dowód dowodzi tylko tego, że zbiór wartości zawiera się w R\<−2,2>. Trzeba jeszcze pokazać inkluzję w drugą stronę.

PW: Liczba w jest wartością funkcji f wtedy i tylko wtedy, gdy istnieje rozwiązanie równania f(x) = w,

	x2+1
(0)		= w, x ≠ 0
	x

x² + 1 = wx x² − wx + 1 = 0

	w		w2
(x −		)2 −		+ 1 = 0
	2		4

	w		w2
(1) (x −		)2 =		− 1
	2		4

Lewa strona jest (dla dowolnych x i w) liczbą nieujemną, a więc rozwiązanie równania (1) istnieje wtedy i tylko wtedy, gdy

	w2
		− 1 ≥ 0,
	4

to znaczy w² ≥ 4. Przezorny sprawdzi, czy rozwiązanie nie jest zerem (bo liczba 0 nie należy do dziedziny funkcji f). Gdyby x = 0 było rozwiązaniem, to musiałoby być

	w		w2
(0−		)2 =		− 1,
	2		4

	w2		w2
		=		− 1,
	4		4

co jest niemożliwe. Odpowiedź: Liczba w jest wartością funkcji f wtedy i tylko wtedy, gdy w∊R\(−2,2).

5-latek: To bardzo się cieszse ze w 1Lo sa funkcje wymierne

Metis: U mnie były w 2 , ale to zależy chyba od podręcznika

5-latek: Czesc Michal Widziales to moje wczorajszse zadanie o tej liczbie xxyy?

Metis: Tak Fajne zadanko. Książka, z której korzystasz jest polecana na końcu książki Brzezińskiego i Bryńskiego, ale wtedy była jeszcze w przygotowaniu

yano: Bardzo dziękuję za pomoc

pigor: ..., myślę, że na poziomie klasy I − szej L.O.przy okazji tematu : równanie kwadratowe i jego pierwiastki (zbliża się koniec roku to w "dobrej" klasie można już w to ... się pobawić) np. tak : −−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	x2+1
dana funkcja wzorem: f(x) = y =		⇔ x2+1 = yx i x≠ 0 ⇒
	x

⇒ równanie kwadratowe x²−yx+1 = 0 z parametrem y , ma pierwiastki (rozwiązanie) zależne od y ⇔ Δ ≥0 ⇔ y²− 4 ≥0 ⇔ ⇔ y² ≥ 4 ⇔ |y| ≥2 ⇔ y≤−2 v y ≥2 ⇔ y∊(−∞;:−2] U [2;+∞) ⇔ ⇔ y = R \ (−2;2) = Z.w_f − szukany zbiór wartości danej funkcji f...