Cw. rachunkowe i wlasnosci liczb
5-latek:
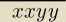
To zadanie jest trudne
Tresc:
Podaj takie dwie cyfry x i y aby liczba xxyy była kwadratem liczby naturalnej
Ta liczba jest zapisana tak w zadaniu
13 maj 20:22
Kacper:
1000x+100x+10y+y=n
2 1≤x≤9 i 0≤y≤9
1100x+11y=n
2
Można sprawdzać wszystkie

lub próbować wymyślić jakiś podstęp

13 maj 20:26
5-latek: Czesc

Po kolei etraz żeby to zalapal
ta liczbe zapisales w postaci 1000x+100x+10y+y i jeśli na być kwadratem liczby naturalnej to
zapisales ze rowna się ona jakies n
2 .
Ale rownie dobrze mogles zapisac ze rowna się ona k
2 czy g
2 (tak?
Teraz wytłumacz mi co to sa za warunki
1≤x≤9 i
0≤y≤9
13 maj 20:32
Kacper: Pierwsze pytania − odpowiedź: tak

No bo mają być cyfry te x i y. Liczba nie może zaczynać się od 0, dlatego x≥1, a potem zera
mogą być

13 maj 20:34
b.: podzielność przez 11 pozwala zmniejszyć liczbę przypadków
13 maj 20:35
5-latek: Tak jakos tez intuicyjnie wyczuwałem ze tak ma być . Wiec dzięki za potwierdzenie mojego
przekonania .

Teraz dodales 1000x+100x = 1100x i 10y+y=11y i zapisales to tak
1100x+11y=n
2 . Dlaczego tak zapisales ? Żeby było lepiej do liczenia przy podstwawianiu
13 maj 20:40
irena_1: 1100x+11y=11(100x+y)
Liczba 100x+y musi dzielić się przez 11 i ostatnia cyfra (y) to 0, 1, 4, 9, 6 lub 5
11(100+y)=11(99x+x+y)
Przez 11 musi dzielić się liczba x+y − takimi liczbami są x=7 i y=4
7744=882
13 maj 20:40
irena_1:
(xxyy)10=1000x+100x+10y+y=110x+11y=11(100x+y)
13 maj 20:41
Mila:
Zadanie z olimpiady.
13 maj 20:46
5-latek: Irenko ten ostatni zapis rozumiem ze to zapisana liczba w systemie dziesiatkowym
Wracajac do postu 20:40
pierwsza linijka zrozumiala następne już nie bardzo
Najpierw to liczba 100x+y musi dzielic się przez 11 (dlaczego ?
i czemu ostatnia cyfra y to 0,1 4 9 6 lub 5
13 maj 20:50
5-latek: Milu nie jest to zadanie z olimpiady
Zadanie ze zbioru Aniela Ehrenfeucht i Olga Stande (tylko oznaczone jako trudne
13 maj 20:53
Mila:
Mam na myśli to, że kiedyś było na olimpiadzie dla uczniów GM.
13 maj 20:57
5-latek: A rozumiem .
Możesz to mi wytlumaczyc (nie chce zagladac do odpowiedzi pewnie tam jest ale chce to zalapac
bez zaglądania (chodzi post 20;50
13 maj 21:01
5-latek: Sugerujac się postem b z 20:35 znalazłem ceche podzielności przez 11
a mianowicie taka
jeśli od sumy liczb stojących na miejscach parzystych odejmiemy sume liczb stjacych na
miejscach nieparzystych i dostaniemy liczbe podzielna przez 11 to ta liczba jest podzielna
przez 11
Tylko czy ta cecha się przyda w tyn zadaniu ?
13 maj 21:09
Mila:
1100x+11y=11(100x+y)
Aby liczba 1100x+11y była kwadratem pewnej liczby naturalnej to musi zachodzic warunek:
100x+y=11*k2
gdzie :
10<k2<90
============= Liczymy na piechotę:
k2 || 11k2
=============
1)16 176 liczba nie jest postaci 100x+y
2) 25 275 nie
3)36 396 nie
4)49 539 nie
5) 64 704=100*7+4 tak, szukana liczba to 11*704=7744
6) 81 891 nie
===================
Poszukiwana liczba to :
112*82=7744
13 maj 21:28
5-latek: Milu na razie dziekuje Ci

Jutro po pracy to sobie dokładnie przeanalizuje .
Potem dopiero wstawie następne zadania
13 maj 21:41
Mila:

13 maj 21:49
b.: > Tylko czy ta cecha się przyda w tyn zadaniu ?
Raczej nie.
13 maj 23:20
5-latek: Milu
Post 21:28 gdzie 10<k<90 dlaczego tak ?
14 maj 17:46
5-latek: miało być 10<k2<90
14 maj 17:50
ZKS:
Wydaje mi się, że 11 * k2 ma być liczbą trzycyfrową, więc jeżeli k2 = 9 to 11 * 9 = 99
tak samo, jeżeli k2 = 91 11 * 91 = 1001.
14 maj 17:57
5-latek: Wybacz ale tego nie rozumiem .
Trudno .
Napiszse CI rozwiązanie ze zbiorku którego tez w pewnym momencie nie rozumiem .
A wiec
xxyy= 1000x+100x+10y+y= 11(100x+y)=k2
Ponieważ 11 jest liczba pierwsza wiec 100x+y musi być wielokrotnoscia 11 ; ale 100x+y= 99x+x+y
wiec x+y musi być wielokrotnoscia 11 .
Po co to tak rozpisali ?
Ponieważ
1≤x≤9
0≤y≤0
========
1≤x+y≤18 a od tego momentu to już calkiem nie weim jak
zatem x+y=11
xxyy= 112(9x+1)=k2
To już rozumiem
Podstawiajac za x kolejno 1,2 3 ...9 stwierdzamy ze jedynie dla 7 liczba 9x+1 jest kwadratem
liczby naturalnej stad x=7 i y=4 szukana liczba to 7744= 882
14 maj 18:23
Mila:
14 maj 18:35
Mila:
Tak , miało być k2, ZKS już napisał dlaczego.
14 maj 18:36
ZKS:
Rozpisali 100x + y na 99x + x + y, aby otrzymać wielokrotność 11.
11 * 9x + x + y zatem zostało nam tylko x + y, które musi być wielokrotnością 11,
więc x + y = 11, ponieważ 1 ≤ x ≤ 9 ∧ 0 ≤ y ≤ 9 (po dodaniu) 1 ≤ x + y ≤ 18,
aby liczba x + y była wielokrotnością 11 musi być równa 11 bo 22 > 18,
czyli nie spełnia założenia x + y ≤ 18.
11 * (100x + y) = 11 * (99x + x + y) = 11 * [11(9x + 1)] = 112(9x + 1).
Rozumiesz?
14 maj 18:37
5-latek: Tak rozumiem
dziekuje CI bardzo

14 maj 18:43
ZKS:
Na zdrowie.
14 maj 18:45
ZKS:
Można by dalej tak zapisać, aby ułatwić szukanie x.
9x + 1 = n2
9x = n2 − 1
9x = (n − 1)(n + 1)
n − 1 = 9 ∨ n + 1 = 9
n = 10 ∨ n = 8
9x + 1 = 100 ∨ 9x + 1 = 64
x = 11 sprzeczność ∨ x = 7
14 maj 19:00
5-latek: No tak

Kiedys
Mila wrzucila w formacie doc na forum zadanka z teorii liczb . Muszse je zanlezc
i pocwiczyc liczenie takich zadań .
14 maj 19:28
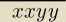 To zadanie jest trudne
Tresc:
Podaj takie dwie cyfry x i y aby liczba xxyy była kwadratem liczby naturalnej
Ta liczba jest zapisana tak w zadaniu
To zadanie jest trudne
Tresc:
Podaj takie dwie cyfry x i y aby liczba xxyy była kwadratem liczby naturalnej
Ta liczba jest zapisana tak w zadaniu
 lub próbować wymyślić jakiś podstęp
lub próbować wymyślić jakiś podstęp 
 Po kolei etraz żeby to zalapal
ta liczbe zapisales w postaci 1000x+100x+10y+y i jeśli na być kwadratem liczby naturalnej to
zapisales ze rowna się ona jakies n2 .
Ale rownie dobrze mogles zapisac ze rowna się ona k2 czy g2 (tak?
Teraz wytłumacz mi co to sa za warunki
1≤x≤9 i
0≤y≤9
Po kolei etraz żeby to zalapal
ta liczbe zapisales w postaci 1000x+100x+10y+y i jeśli na być kwadratem liczby naturalnej to
zapisales ze rowna się ona jakies n2 .
Ale rownie dobrze mogles zapisac ze rowna się ona k2 czy g2 (tak?
Teraz wytłumacz mi co to sa za warunki
1≤x≤9 i
0≤y≤9
 No bo mają być cyfry te x i y. Liczba nie może zaczynać się od 0, dlatego x≥1, a potem zera
mogą być
No bo mają być cyfry te x i y. Liczba nie może zaczynać się od 0, dlatego x≥1, a potem zera
mogą być 
 Teraz dodales 1000x+100x = 1100x i 10y+y=11y i zapisales to tak
1100x+11y=n2 . Dlaczego tak zapisales ? Żeby było lepiej do liczenia przy podstwawianiu
Teraz dodales 1000x+100x = 1100x i 10y+y=11y i zapisales to tak
1100x+11y=n2 . Dlaczego tak zapisales ? Żeby było lepiej do liczenia przy podstwawianiu
 Jutro po pracy to sobie dokładnie przeanalizuje .
Potem dopiero wstawie następne zadania
Jutro po pracy to sobie dokładnie przeanalizuje .
Potem dopiero wstawie następne zadania


 Kiedys Mila wrzucila w formacie doc na forum zadanka z teorii liczb . Muszse je zanlezc
i pocwiczyc liczenie takich zadań .
Kiedys Mila wrzucila w formacie doc na forum zadanka z teorii liczb . Muszse je zanlezc
i pocwiczyc liczenie takich zadań .