dowody lsia:  1. W trapezie ABCD (AB || CD) przekątne AC i BD przecinają się w punkcie O takim, że AO : OC = k (k>1). Pole trójkąta AOD jest równe P. Wyznacz w zależności od P i k pole trapezu ABCD.  2. Wykaż, że jeżeli dwie liczby rzeczywiste x i y spełniają warunek x + y = 2, to x⁴+y⁴≥2 Mam takie dwa dowody, ktos cos?

irena_1:

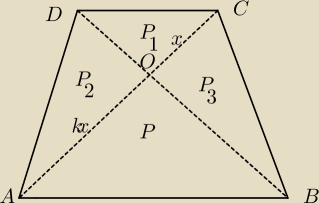
	1		1
Trójkąt COD jest podobny do AOB w skali		, więc P1=		*P
	k		k2

Trójkąty AOD i COD mają wspólną wysokość opuszczoną na prostą AC, więc stosunek ich pól jest równy stosunkowi długości podstaw

	1
P2=k*P1=		*P
	k

Trójkąty P₂ i P₃ mają to samo pole

	1		1		1		1
PABCD=P+2*		*P+		*P=P*(1+2*		+		)=
	k		k2		k		k2

	k2+2k+1		k+1
=		*P=(		)2*P
	k2		k

irena_1: Dla każdej pary liczb rzeczywistych x, y zachodzi (x−y)²≥0 x²−2xy+y²≥0 x²+y²≥2xy x+y=2 (x+y)²=4 x²+y²+2xy=4 x²+y²+x²+y²≥4 i 2xy+2xy≤4 2(x²+y²)≥4 i 4xy≤4 x²+y²≥2 i xy≤1 x⁴+y⁴=(x²+y²)²−2x²y²=(x²+y²)²−2(xy)²≥2²−2*1=4−2=2

Eta: @irena W zad.1 błędnie odczytana treść P(AOD)= P

Kacper: Zadanie 2 Z nierówności między średnią kwadratową a arytmetyczną dla liczb x² i y² mamy:

	(x2)2+(y2)2		x+y
√		≥		=1
	2		2

x4+y4
	≥1
2

x⁴+y⁴≥2 c.k.d

Kacper: Nie polecam tego rozwiązania, bo zepsułem

Eta: Z nierówności między średnią potęgową i średnią arytmetyczną :

	x4+y4		x+y
4√		≥		= 1 |4
	2		2

x⁴+y⁴≥2 c.n.u

lsia: Dziekuje wszystkim pieknie!