ekstrema lokalne dzikiewensze: Wyznaczyć ekstrema lokalne oraz przedziały monotoniczności funkcji f(x)=x²*e^−x2

Mila: Tu masz podobne zadanie. http://www.math.com.pl/analiza-matematyczna-1/badanie-przebiegu-zmiennosci-funkcji/

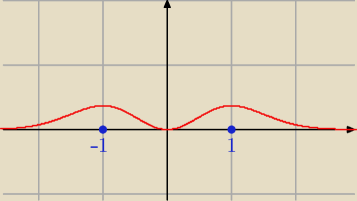
Janek191: Np. ekstrema funkcji f f(x) = x²*e^−x2 Df = ℛ f'(x) = 2 x*e^−x2 + x²*e^−x2*(−2x) = 2 x*e^−x2 − 2x³*e^−x2 = 0 ⇔ ⇔ e^−x2*( 2 x − 2 x³) = 0 ⇔ 2x*( 1 − x²) = 0 ⇔ x = 0 lub x = − 1 lub x = 1 oraz f'' (x) = ( 2 − 6 x²)*e^−x2 − 2 x*e^−x2*( 2 x − 2 x³) = ( 4 x⁴ − 10 x² + 2)*e^−x2 więc f''( − 1) < 0 ⇒ f ma maksimum lokalne f''( 0) > 0 ⇒ f ma minimum lokalne f'' (1) < 0 ⇒ f ma maksimum lokalne