 nie pomagać
dla Anki:
załóżny, że jest to nasz sześciokąt
nie pomagać
dla Anki:
załóżny, że jest to nasz sześciokąt  no troszkę krzywy
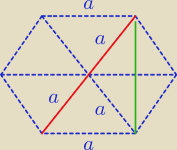
sześciokąt to inaczej sześć trójkątów równobocznych o dł. boku a
czerwona (dłuższa przekątna): x+√3
zielona (krótsza przekątna) : x
,czyli 2a=x+√3
z trójkąta prostokątnego:
a2+x2=(x+√3)2
no troszkę krzywy
sześciokąt to inaczej sześć trójkątów równobocznych o dł. boku a
czerwona (dłuższa przekątna): x+√3
zielona (krótsza przekątna) : x
,czyli 2a=x+√3
z trójkąta prostokątnego:
a2+x2=(x+√3)2
| x+√3 | ||
oraz wiemy, że a= | ||
| 2 |
| x+√3 | ||
( | )2+x2=x2+2√3x+3
| |
| 2 |
| x2+2√3x+3 | |
=2√3x+3 /*4
| |
| 4 |
| 6{3}−12 | ||
x1= | = 3√3−6 ≠ nie zgodne z założeniem, bo długość nie może być ujemna
| |
| 2 |
| 6{3}+12 | ||
x2= | = 3√3+6
| |
| 2 |
| x+√3 | ||
a= | ||
| 2 |
| 3√3+6+√3 | ||
a= | ||
| 2 |
 nie to nie jest jedyny sposób rozwiązania tego zadania:
sposób II
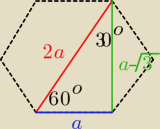
pamiętasz trójkąt 30o, 60o ,90o tam była właśnie taka zależność:
w naszym przypadku mamy
2a=x+√3
a√3=x
mamy układ równań więc go rozwiążmy
2a=a√3+√3
2a−a√3=√3
a(2−√3)=√3
nie to nie jest jedyny sposób rozwiązania tego zadania:
sposób II
pamiętasz trójkąt 30o, 60o ,90o tam była właśnie taka zależność:
w naszym przypadku mamy
2a=x+√3
a√3=x
mamy układ równań więc go rozwiążmy
2a=a√3+√3
2a−a√3=√3
a(2−√3)=√3
| √3 | ||
a= | ||
| 2−√3 |
| √3 | ||
a*1= | *1
| |
| 2−√3 |
| √3 | 2+√3 | |||
a*1= | * | |||
| 2−√3 | 2+√3 |
| √3*(2+√3) | ||
a= | ||
| (2−√3)(2+√3) |
| 2√3+3 | ||
a= | ||
| 4−3 |