matematyka ewa25: wyraz ogolny ciagu an dany jest wzorem an=4/n²(1+2+3+...+n)zbadaj monotonicznosc ciagu an

J: zapis niejasny

ewa25: tylko tyle

===: zapisałaś

	4
an=		... tak ma być
	n2(1+2+3+...+n)

czy:

	4
an=		(1+2+3+...+n)
	n2

ewa25: tak

ewa25: ten drugi

J:

	2(n+1)
an =		.. i lczysz: an+1 − an =
	n

ewa25: a dalej

J:

	2(n+2)		2(n+1)
oblicz:		−		= ...?
	n+1		n

===:

	4		1+n		4n+4n2		2n+2		2
an=		*		n=		=		=2+		... i wnioskuj −
	n2		2		2n2		n		n

ewa25: tzn j

Maks Paradys: ciemność widzę

ewa25: bardzo smieszne

ewa25: nie wszyscy musz rozumiec matematyke

ewa25: kazdy jes z czego innego dobry

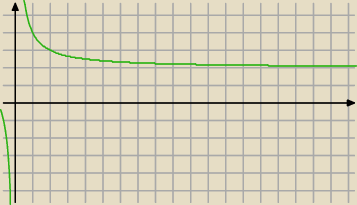
===: Przedstawiłem sposób troszkę inny niż a_n+1−a_n

	2
Zauważ, że f(n)=2+		to funkcja wymierna
	n

Jej wykres zobacz tu https://matematykaszkolna.pl/strona/157.html Kolejne wyrazy ciągu a_n "układają się" na wykresie f(n) dla n∊N₊ f(n)− jest malejąca ... zatem a_n ...?

Maks Paradys: "nie wszyscy muszą rozumieć matematykę" − czy także ktoś, kto chce mieć wykształcenie na określonym poziomie?

===:

	an+1
możesz też przeanalizować
	an

2(n+1)+2   n+1		2n+4		n
	=		*		=...
2n+2   n		n+1		2(n+1)

J:

	1		1
tutaj leży problem z dodaniem:		+		... , a Ty proponujesz analizę
	2		3

===: ... chyba już zainteresowanie prysło − Ewa jest dobra w innych dziedzinach −

J:

ewa25: dzieki

===: −

ewa25: mam tylko zbadac

ewa25:

===: wszystko zaczyna się od diagnozy −

ewa25: Aha