Bardzo proszę o pomoc, PILNE
Szewczu: Na Δ równobocznym o boku=1 opisano okrąg wykaż, że dla dowolnego M, tego okręgu zachodzi
równość |MA|2 + |MB|2 + |MC|2 = 2
zadanie trzeba rozwiązać stosując wektory, bardzo proszę o pomoc
12 maj 23:33
Szewczu: Błagam was ludzie
13 maj 00:00
Kacper:
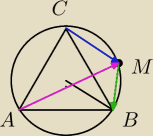
Rysunek

Jeśli Punkt M pokrywa się z którymś z wierzchołków, to tezę widać od razu

Jeśli M≠A i M≠B i M≠C, to:
czworokąt ABCM jest wpisany w okrąg i zachodzi twierdzenie Ptolemeusza:
|AM|*|BC|=|AC|*|BM|+|AB|*|CM|
|AM|=|BM|+|CM| |
2
|AM|
2=|BM|
2+|CM|
2+2|BM|*|CM| (*)
Z tw. cos w trójkącie BMC mamy:
1
2=|CM|
2+|BM|
2−2|CM|*|BM|*cos(∡CMB)=|CM|
2+|BM|
2+|CM|*|BM|
2=2(|CM|
2+|BM|
2+|CM|*|BM|) (**)
(**) − (*)
|AM|
2+|BM|
2+|CM|
2=2 c.k.d
Nie bardzo chce mi się myśleć nad innym rozwiązaniem.
13 maj 00:03
Kacper:
Skąd to zadanie?
13 maj 00:05
Szewczu: Dostałem od mojego profesora. Dziękuję bardzo za pomoc

13 maj 00:11
Kacper:
Zapytaj o dowód z użyciem wektorów i napisz do mnie 8959267.
Chyba, że wcześniej sam go sobie wymyślę

13 maj 00:14
Kacper:

13 maj 09:22
Szewczu: masz?
13 maj 12:29
Mila:
To studia, czy LO?
13 maj 18:10
Kacper:
Mila masz może jakiś pomysł na to zadanie inny niż mój?

− To liceum.
13 maj 19:32
YushokU: A jakby to wrzucić w układ współrzędnych? Nie podejmuję się rozwiązania, bo jutro ustny polski,
ale będę śledził.
13 maj 21:21
Kacper:
Yushoku zapewne pójdzie, ale autor chciał rozwiązania przy użyciu wektorów i nad nim
myślę.
Zresztą cięzko powiedzieć o jakie zastosowanie wektorów dokładnie chodziło.
13 maj 21:25
PW: Może o taką sztuczkę, której nie umiem dokończyć ale jest to jakiś pomysł:
Niech S oznacza środek okręgu opisanego.
MA→ = MS→+SA→,
a więc po "podniesieniu skalarnie do kwadratu"
MA2 = MS2 +2MS→ oSA→ + SA2
i analogicznie
MB2 = MS2 +2MS→ oSB→ + SB2
MC2 = MS2 +2MS→ oSC→ + SC2.
Wiadomo, że
MS2 = 1.
zatem
MA2 +MB2 +MC2 = 3 + 2MS→ o(SA→+SB→+SC→).
Dalej coś się zaciąłem, ale chyba blisko.
13 maj 21:43
PW: A jeszcze tu strzeliłem głupstwo:
MS2
wcale nie jest równe 1, bo promień okręgu opisanego jest równy ...
13 maj 21:46
PW: | | 1 | |
MS2 = SA2=SB2=SC2 = |
| , a więc po zsumowaniu tych trzech równości otrzymamy: |
| | 3 | |
| | 1 | |
MA2+MB2+MC2 = 6· |
| +2MS→ o(SA→+SB→+SC→) |
| | 3 | |
MA
2+MB
2+MC
2 =
2 + 2MS
→ o(SA
→+SB
→+SC
→),
czyli wystarczy pokazać, że suma wektorów w nawiasie jest wektorem zerowym.
13 maj 23:22
 Rysunek
Rysunek  Jeśli Punkt M pokrywa się z którymś z wierzchołków, to tezę widać od razu
Jeśli Punkt M pokrywa się z którymś z wierzchołków, to tezę widać od razu  Jeśli M≠A i M≠B i M≠C, to:
czworokąt ABCM jest wpisany w okrąg i zachodzi twierdzenie Ptolemeusza:
|AM|*|BC|=|AC|*|BM|+|AB|*|CM|
|AM|=|BM|+|CM| |2
|AM|2=|BM|2+|CM|2+2|BM|*|CM| (*)
Z tw. cos w trójkącie BMC mamy:
12=|CM|2+|BM|2−2|CM|*|BM|*cos(∡CMB)=|CM|2+|BM|2+|CM|*|BM|
2=2(|CM|2+|BM|2+|CM|*|BM|) (**)
(**) − (*)
|AM|2+|BM|2+|CM|2=2 c.k.d
Nie bardzo chce mi się myśleć nad innym rozwiązaniem.
Jeśli M≠A i M≠B i M≠C, to:
czworokąt ABCM jest wpisany w okrąg i zachodzi twierdzenie Ptolemeusza:
|AM|*|BC|=|AC|*|BM|+|AB|*|CM|
|AM|=|BM|+|CM| |2
|AM|2=|BM|2+|CM|2+2|BM|*|CM| (*)
Z tw. cos w trójkącie BMC mamy:
12=|CM|2+|BM|2−2|CM|*|BM|*cos(∡CMB)=|CM|2+|BM|2+|CM|*|BM|
2=2(|CM|2+|BM|2+|CM|*|BM|) (**)
(**) − (*)
|AM|2+|BM|2+|CM|2=2 c.k.d
Nie bardzo chce mi się myśleć nad innym rozwiązaniem.



 − To liceum.
− To liceum.