Wyznacz zbiór wartości funkcji. pp: f(x)=|3sinx|−1 Jak się za to zabrać jeśli mam wartość bezwzględną?

wmboczek: normalnie −1≤sinx≤1 ⇒0≤|sinx|≤1 obniżenie o 1 i Z_w=<−1;0>

wmboczek: a jak było Z_w=<−1;2>

pp: też tak myślałem dopóki nie spojrzałem na odpowiedzi.. tam jest Zw=<−1,2>

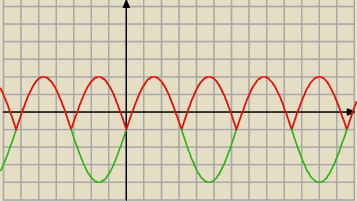
5-latek: Zielony y=3sinx−1 czerwony y=|3sinx|−1 Odpowiedz sobie na pytanie . Co robi z wykresem wartość bezwzgledna ? jaka nie może być wartość bezwzgledna ? Wiec co robisz zz ta czescia wykresu która znajduje się pod osia OX ?

ZKS: −1 ≤ sin(x) ≤ 1 / * 3 −3 ≤ 3sin(x) ≤ 3 0 ≤ |3sin(x)| ≤ 3 −1 ≤ |3sin(x)| − 1 ≤ 2.

pp: 5−latek: Wiem że nie może być ujemna i że to co pod spodem się odbija tylko nie wiedziałem co z w tym przypadku mam z tym zrobić ZKS: Czyli wartość bezwzględna dopiero potem.. dzięki

5-latek:

ZKS: Jeżeli byś przed wartością bezwzględną odjął tę jedynkę miałbyś funkcje postaci f(x) = |3sin(x) − 1|.

pp: tak tak rozumiem dzięki jeszcze raz