Zaznacz na płaszczyźnie zbiór punktów, których współżędne spełniają układ: Nei:

⎧	2x + y ≤ 7
⎩	y ≥ 2x + 9

Proszę o rozwiązanie, tak bym mógł zobaczyć, co się robi po kolei. Dziękuję.

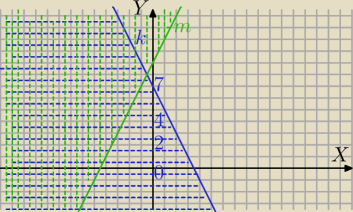
Mila: y≤−2x+7 punkty płaszczyzny leżące na prostej k: y=−2x+7 i poniżej tej prostej y≥2x+9 punkty płaszczyzny leżące na prostej m:y=2x+9 i powyżej tej prostej Rozwiązanie część wspólna zaznaczonych obszarów

5-latek: Dziekuje bardzo już będę wiedział

Mila:

Nei: Co się dzieje z tymi 2x?

Mei: 2x poszły w długą

Nei: Można to jakoś rozpisać?

Kei: Nie da się współżędnych rozpisać

Mila: Nie rozumiem Twojego pytania. Przecież masz równania prostych, które narysowałam.

Nei: Tzn, dlaczego akurat tak przebiegają te proste? Wiem, że jeżeli y ≤, to punkty znajdują się poniżej tej prostej. Natomiast, jeżeli y ≥, to punkty znajdują się powyżej prostej. Z tego co napisał/a @Mei iksy idą w długą, więc skąd z tej 7 i 9 te proste?

Mila: Aby narysować prostą to musisz mieć dwa różne punkty przez które przechodzi . 2x + y ≤ 7 przekształcamy nierówność y≤−2x+7 Punkty należące do prostej: y=−2x+7 (0,7) , (1,5) teraz narysuj to na kartce y ≥ 2x + 9 Druga prosta : y=2x+9 (0,9), (1,11) (−1,7) Narysuj.

Nei: To znaczy, że jak mam: 3x−1 ≤ y+2, to przekształcam: −y ≤ 2+1−3x −y ≤ −3x+3 y ≥ 3x−3. Punkty należące do prostej: y=3x−3 (0,3), (1,2) 2y+3 > x−1 2y > x−1−3 2y > x−4 (0,4), (1,7), (−1,2) ?

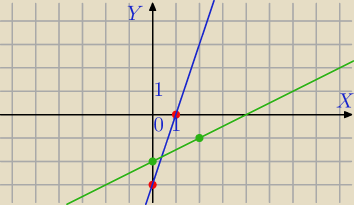
Mila: y=3x−3 x=0 to y=3*0−3=−3 jest punkt (0,−3) x=1 to y=3*1−3=0 jest punkt (1,0) Przez te punkty przechodzi prosta y=3x−3 W drugim nie wyznaczyłaś zmiennej y. 2y=x−4 /:2

	1
y=		x−2
	2

(0,−2), (2,−1) punkty wykresu