funkcje trygonometryczne zmiennej rzeczywistej Adamxd: Jak wyznaczyc zbior wartosci tych funkcji

	1
a)
	sinx

	1
b)
	cos2−2cosx−8

	−3
c)
	cosx

7
sin2−sinx−12

Adamxd: pomoze ktoś mam taka załamke w tym że masakra

Adamxd:

prosta:

	1
a) f(t)=		i t∊<−1,0)∪(0,1>
	t

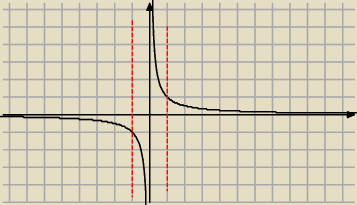
Kacper: Zrobię ci pierwszy przykład. Trzeci analogicznie. g(x)=sinx, −1≤sinx≤1

	1
f(x)=		, Df=<−1,0)∪(0,1>
	g(x)

Rysujemy hiperbolę i odczytujemy zbiór wartości w określonej dziedzinie. Zw_f=(−∞,−1>∪<1,+∞)

prosta: a) stąd f(t)∊(−∞,−1>∪<1,+∞)

Adamxd: jakto jakto przecierz bedzie ten przedzial chyba <−1,0)∪(0,1> , no rysowalem ta hiperbole i od jej zbioru wartosci odlolem zbior wartosci funkcji sinus

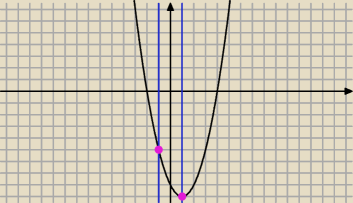
prosta: c) −1≤cosx≤1 ⇒ f(1) ≤cos²−2cosx−8≤f(−1) i f(x)=x²−2x−8 −9≤cos²−2cosx−8≤−5

	1		1		1
stąd: −		≤		≤ −
	5		cos2−2cosx−8		9

Adamxd: dlaczego te dwie linie są pionowe a nie poziome

Adamxd: Ta kwestia nurtuje mnie za przeproszeniem fchui od 3 godzin

Adamxd: moglby mi to ktos wyjasnic?

Adamxd:

prosta: ad.a)

	1
rozpatrujesz funkcję y=		w dziedzinie <−1,0)∪(0,1>
	x

prosta: ad.c) 1. początkowo rozpatrujemy funkcję f₁(x)=x²−2x−8 w dziedzinie <−1,1> otrzymujemy zbiór wartości <−9,−5>

	1
2. następnie rozpatrujemy funkcję f2(x)=		w dziedzinie <−9, −5>
	x

	1		1
otrzymujemy zbiór wartości < −		, −		>
	5		5

Mamy w tym zadaniu złożenie trzech funkcji

prosta:

	1		1
poprawka < −−		,−		>
	5		9

Adamxd: no ale czemu dziedzina <−1,0)∪(0,1> nie bedzie zbiorem wartosci dla 1/sinx

Adamxd: ?

52: dla sinx ZWf <−1,1>

	1
dla		ZWf <−1,0)∪(0,1>
	sinx

a czemu bez 0 ? Ponieważ dziedzina... kπ, k∊C rozumiesz teraz ?

prosta: Adamxd, post 17.12

	1
1. gdy t∊(0,1> to		∊<1,+∞)
	t

(odwrotności liczb dodatnich mniejszych od 1 są liczbami większymi od1)

	1
stąd gdy sinx∊(0,1> to		∊<1,+∞)
	sinx

prosta: i podobnie

	1
gdy sinx∊<−1,0) to		∊(−∞,−1>
	sinx

Adamxd: ale czemu zwbior wartosci tej funkcji odwrotnej jest taki ZWf <−1,0)∪(0,1>

prosta: przecież sinus ma wartości z przedziału <−1,1> i nie może być równy zero, gdyż występuje w mianowniku ułamka

Adamxd: aaa