| 4 | ||
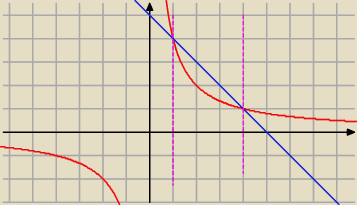
Oblicz pole ograniczone funkcjami y=−x+5 i y= | ||
| x |
| 4 | ||
∫(−x+5− | )dx | |
| x |
| 4 | dx | 1 | ||||
∫(−x+5− | )dx=−∫xdx+5∫dx−4∫ | =− | x2+5x−4ln|x|+C | |||
| x | x | 2 |
| 1 | ||
[− | x2+5x−4ln|x|]=12−4ln4−4,5=7,5−4ln4 | |
| 2 |
| 15 | ||
W odpowiedzi | −8ln2 ? | |
| 2 |
| 15 | ||
Oczywiście, | =7,5 | |
| 2 |
| 15 | |
− 8ln2 = 7,5 − 2*4ln2 = 7,5 − 4ln4 ..  | |
| 2 |
| 4 | ||
...−4ln | =−4ln4=−4ln22=−8ln2 | |
| 1 |
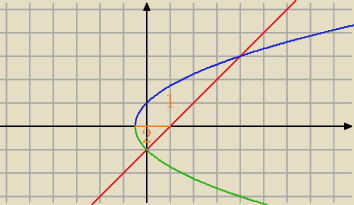 y2= 2x +1 x−y−1= 0
y=√2x+1 lub y=−√2x+1 y=x−1
Czyli dzielę na dwa pola ?
y2= 2x +1 x−y−1= 0
y=√2x+1 lub y=−√2x+1 y=x−1
Czyli dzielę na dwa pola ?
| 1 | 1 | |||
g(x) = | x2 − | |||
| 2 | 2 |
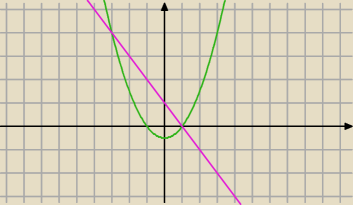 sorry... <−3,1>
sorry... <−3,1>
 Jak zmieniać granice całkowania ?
Jak zmieniać granice całkowania ?
| 1 | 1 | |||
y2 = 2x + 1 ⇔ 2x = y2 − 1 ⇔ x = | y2 − | .. .i zamieniasz zmienne  | ||
| 2 | 2 |