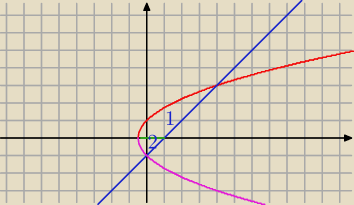
obszar Lukas: Pole obszaru y²=2x+1 y=x−1 y=√2x+1 y=−√2x+1 P₁=∫(√2x+1−x+1)dx w granicach całkowania 0,5−4 P₂=∫(x−1+√2x+1)dx w granicach 0,5−1 Zgadza sie

Lukas: ?

Mila: Skąd to 0.5? Obszar normalny względem OY. 2x=y²−1, Granice :

	1		1
x=		y2−
	2		2

x=y+1 −1≤y≤3

	1		1		3		1
−1∫3(y+1−		y2+		)dy=−1∫3(y+		−		y2)dy=
	2		2		2		2

	1		3		1
=[		y2+		y−		y3]−13=
	2		2		6

	1		3		1		1		3		1
=		*9+		*3−		*27−(		−		+		)=
	2		2		6		2		2		6

	9		1		16
=		+1−		=
	2		6		3

Lukas: Przecież ten czubek wychodzi na −0,5

Mister Ed: O! Kolejny czubek

Lukas:

Lukas: Mila skąd masz obszar −1 do 3?

Mila: y²=2x+1 y=x−1 (x−1)²=2x+1 x²−2x+1=2x+1 x²−4x=0 x*(x−4)=0 x=0 to y=−1 lub x=4 to y=4−1=3 (0,−1), (4,3) punkty przecięcia wykresów.

Lukas: Dziękuję !

Mila:

Lukas: ?