oblicz długość przeciwprostokątnej w zależności od wysokości i dwusiecznej kąta zakręcona: cześć, zadania: w trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego ma długość h , zaś dwusieczna kąta prostego ma długość d . Oblicz długość przeciwprostokątnej tego trójkąta w zależności od h i d.

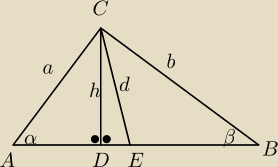
irena_1: |AD|=x |BD|=y |DE|=t |< ACE|=|<BCE|=45⁰ |AB|=c=x+y

x+t		d		d		ad
	=		=		=
sin450		sinα		ha		h

	√2		ad
x+t=		*
	2		h

y−t		d		d		bd
	=		=		=
sin450		sinβ		hb		h

	√2		bd
y−t=		*
	2		h

	√2d
x+t+y−t=x+y=		(a+b)
	2h

	√2d
c=		(a+b)
	2h

Z pola trójkąta:

ab		ch
	=
2		2

ab=ch

	2d2		d2
c2=		(a2+b2+2ab)=		(c2+ch)
	4h2		2h2

	d2
c2=c*		(c+h)
	2h

	d2		d2
c=		*c+
	2h2		2h

	d2		d2
c(1−		)=
	2h2		2h

	2h2−d2		d2
c*		=
	2h2		2h

	2h2−d2
c*		=d2
	h

	hd2
c=
	2h2−d2

prosta: liczę podobnie:

	ab√2		ab√2
1. dwusieczna d=		⇒ a+b=
	a+b		d

	ab
2. wysokość h=		⇒ ab=hc
	c

	hc√2
stąd a+b=
	d

3. (a+b)²=a²+b²+2ab

	2h2c2
		=c2+2hc
	d2

2h²c² =}d²c²+2hcd² c(2h²−d²)=2hd²

	2hd2
c=
	2h2−d2

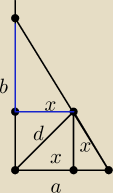prosta: dwusieczną wyznaczam korzystając z podobieństwa:

a		x
	=
b		b−x

	ab
x=
	a+b

	ab√2
d=x√2 ⇒ d=
	a+b