Planimetria RoxySS: Oblicz długość boku |BC| trójkąta |ABC| , wiedząc że |AB|=1 , |AC|=3 i kąt |ABC|=30 stopni

RoxySS: No rozumiem że musimy użyć tw. sinusów czyli będzie 3/sin30 = 1/sinγ dalej 3sinγ=sin30 sin 30 =1/2 3sinγ=1/2 / : 3 sinγ=1/6 i co dalej jak w przybliżeniu nie ma 0,166666667 ?

RoxySS: up

RoxySS: up

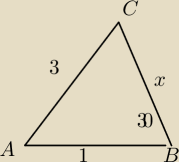
5-latek: Należy dwa razy zastosować twierdzenie sinusow

3		1
	=		wylicz ztego sinC i sprawdzić jaki to będzie kat w tablicach np.
sin30		sinC

Kat A= 180−(30^o+kątC)

x		3
	=		i wylicz z tego x
sina		sin30

RoxySS: Tak ale w tablicy właśnie nie mogę znaleźć 1/6

5-latek: W dokładniejszych tablicach matematycznych będzie to 9,30^o

RoxySS: A w niedokładnych 10 mogę użyć ?

5-latek: Popatrzylem na tablice tangensów zamiast sinusow ale dla małych katow sinα≈tgα Będzie roznica o 10' wiec tak zostawny wiec A= 140,30^o wiec ze ze wzorow redukcyjnycjh sin140,30= sin(180−39,3)= sin39,30 ^o a sin 39,30^o=0,636 Teraz licz

5-latek: Mysle ze możesz uzyc 10 ^o

RoxySS: Dobra no to mam kąt 3/sin30 i x/sin140 co dalej bo raczej mam problem duży z matematyką

5-latek: https://matematykaszkolna.pl/strona/430.html patrz tutaj No to sin140^o to przecież rowna się sin140=(sin180−40)= sin40 patrz na wzor sin(180−α)= sinα a sin40 odcztaj z tablic

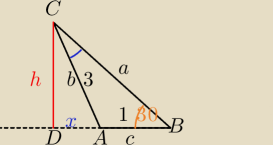
Mila: Bez tw. sinusów W ΔCDB:

	1		h
sin30o=		=
	2		a

	1
h=		a
	2

	x+1
cos30=
	a

√3		x+1
	=
2		a

	a√3
x+1=
	2

	a√3
x=		−1
	2

	3a2		a√3
x2=		−2*		+1
	4		2

	3a2−4a√3+4
x2=
	4

W ΔCDA: z tw. Pitagorasa 3²=h²+x²

	a2		3a2−4a√3+4
9=		+
	4		4

po rozwiązaniu:

	√3+√35
a=
	2

Zaraz napiszę z zast. tw. sinusów

5-latek: Witam Milu Pozdrawiam Z drugiej strony Krzysiek . taki miałem tez nick przy 1 rerejertacji

Mila: II sposób:

3
	=2R
sin30

2R=6

3		1
	=
sin30o		sinγ

	1
Stąd sinγ=
	6

a
	=2R
sin(180−(30+γ)

a=6*sin(γ+30) cos²γ=1−sin²γ

	1
cos2γ=1−
	36

	√35
cosγ=
	6

	1		√3		1		√35
sin(γ+30)=sinγ*cos30+sin30 *cosγ=		*		+		*		=
	6		2		2		6

	√3+√35
=
	12

	√3+√35
a=6*
	12

	√3+√35
a=
	2

===============

Mila: Witaj .