Rówananie
Lukas:
e−x=−2
Zapomniałem jak się to robiło, ktoś przypomni ?
10 maj 00:16
jakubs: Ojoj to coś z zespolonymi
10 maj 00:22
Lukas:
Nie raczej, czekam na pomoc.
10 maj 00:25
jakubs:
dalej nie wiem
10 maj 00:25
jakubs: Malnij sobie wykres e
−x i zobaczysz, że tam będą ℤ
Dobranoc
10 maj 00:26
kyrtap: x ∊ ∅
10 maj 00:26
Lukas:
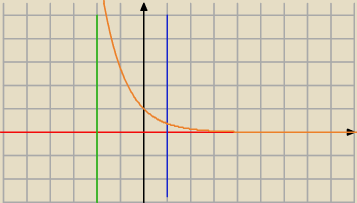
Bo muszę obliczyć pole obszaru
y=e
−x y=0 x=−2 x=1
Dobra jednak nie potrzebuję tego liczyć
Dzięki Panowie
10 maj 00:28
Lukas:
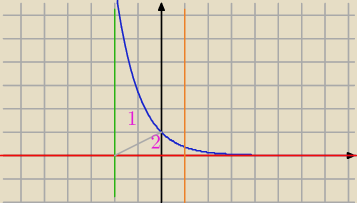
Muszę to pole podzielić na dwa pola. Czy taki podział jest ok ?
10 maj 00:36
Lukas:
Ok, zrobione
10 maj 00:40
Lukas:
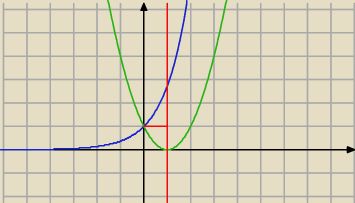
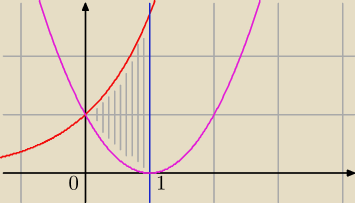
Teraz mam y=e
x x=1 y=(x−1)
2
Muszę to pole podzielić na dwa ? Tak jak na rysunku ?
10 maj 00:55
Lukas:
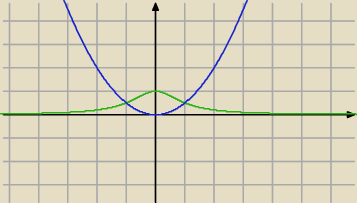
10 maj 01:15
Lukas:
1
−1
| | dx | | 1 | | 1 | |
∫ |
| − |
| ∫x2dx=arctgx− |
| x3+C |
| | x2+1 | | 2 | | 6 | |
1
| | 1 | | 1 | | 1 | |
[arctgx− |
| x3]=[arctg(1)− |
| ]−[arctg(−1)+ |
| ] |
| | 6 | | 6 | | 6 | |
−1
| | π | | 1 | | π | | 1 | | π | | 1 | |
= |
| − |
| + |
| − |
| = |
| − |
| |
| | 4 | | 6 | | 4 | | 6 | | 2 | | 12 | |
| | π | | 1 | |
w odpowiedzi jest |
| − |
| ? |
| | 2 | | 3 | |
więc gdzie błąd ?
10 maj 01:34
Lukas: ?
10 maj 01:42
Saizou :
| | 1 | | 1 | | 2 | | 1 | |
W dodawaniu ułamków − |
| − |
| =− |
| =− |
| |
| | 6 | | 6 | | 6 | | 3 | |
a po co dzielić to na wa pola ? Przecież możesz zapisać to jako (w przedziale [0,1])
| | 1 | |
P=∫ex−(x−1)2 dx=ex− |
| (x−1)3 |01 |
| | 3 | |
| | 1 | | 1 | | 1 | | 4 | |
=e1− |
| (1−1)3−[e0− |
| (0−1)3]=e1−1− |
| =e1− |
| |
| | 3 | | 3 | | 3 | | 3 | |
10 maj 08:50
Lukas:
Nie można policzyć jednego pola, bo wtedy masz ogranicznenie 3 funkcjami
10 maj 10:05
Saizou :
prosta o równaniu x=1 nie jest funkcją zmiennej x
taka prosta wyznacza nam w tym przypadku prawą granicę całkowania
10 maj 10:08
Lukas:
Dzięki po raz kolejny, mam jeszcze kilka przykładów
10 maj 10:22