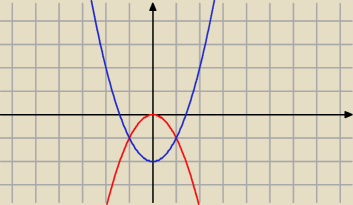
Pole obszaru Lukas: Pole obszaru pomiędzy y=−x² i y=x²−2 1 1 P=∫[x²−2+x²]dx=∫(2x²−2)dx −1 −1

	2
∫(2x2−2)dx=2∫x2−2∫x=		x3−2x+C
	3

	2		2		2		8
[		x3−2x]=[		*1−2]−[		*(−1)3+2]=−
	3		3		3		3

Co jest nie tak ? Pole nie może wyjść ujemne przeca

Saizou : wyrażenie podcałkowe −x²−(x²−2)=2−2x²

Lukas: Dzięki mistrzu !

Saizou : a no proszę proszę, choć mistrz ze mnie żaden

Lukas: Ale nadal mi się nie zgadza

Saizou : nie będę pisał przedziału ale policzę całkę od 0 do 1 i domnożę ją razy 2

	1
∫−x2−(x2−2)dx=∫−2x2+2dx=2∫1−x2 dx=2(∫dx −∫x2dx)=2(x−		x3)
	3

domnażając całkę i licząc wartości na końcach przedziału otrzymamy

	1		1		8
4*(x−		x3)|01=4(1−		−0+0)=
	3		3		3

Lukas: wyszło już

Mila:

	2
−1∫1 (−x2−(x2−2)) dx=−1∫1 (2−2x2)dx=[2x−		x3]−11=
	3

	2		2		2		2		4		8
=2−		−(−2+		)=2−		+2−		=4−		=
	3		3		3		3		3		3

Saizou : swoją drogą zauważ że jeśli f(x) leży "wyżej" niż g(x) to pole to ∫f(x)−g(x)dx na przedziale [a,b] a jeśli nie chcemy się bawić w określanie która funkcja jest "wyżej" wystarczy wziąć moduł z wyrażenia f(x)−g(x)

Lukas: Mila Tobie również dziękuję, źle spojrzałem i stąd mój błąd.