Geometria jony: W trójkącie prostokątnym, współrzędne wierzchołków kątów ostrych wynoszą (1;−2) oraz (2;5). Znajdź współrzędne wierzchołka kąta prostego wiedząc, że znajduje się on na prostej y = 4x + 8

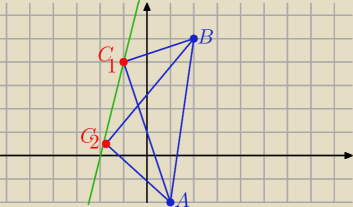
Eta: A(1,−2) , B(2,5) , C(x, 4x+8) z prostopadłości wektorów AB⊥AC → → AB=[2−x, −4x−3] i AC =[1−x, −4x−10] iloczyn skalarny =0 (2−x)(1−x)+(4x+3)(4x+10)=0⇒ ......... 17x²+49x+32=0 , Δ=225, √Δ=15

	32		8
x= −1 lub x= −		to y= 4 lub y=
	17		17

	32		8
odp: C1(−1,4) , C2=(−		,		)
	17		17

Gustlik: Eta, o tym samym pomyślałem, tylko tzw. "mądrzy inaczej" ograniczyli wektory do minimum, a iloczyn skalarny i wektorowy to zniknął nawet z rozszerzenia. Wg mnie cały rachunek wektorowy powinien BYĆ OBOWIĄZKOWY NA POZIOMIE PODSTAWOWYM ! Bo jest banalnie prosty. Szczerze mówiąc wektory są proste nawet dla słabych uczniów z podstaw, to jest dla nich o wiele łatwiejsze niż zadania na dowód. Nie wiem czemu to dowody, które potrafią przyprawić o zawał serca nawet niektórych uczniów z rozszerzeń (choć na rozszerzeniach jest zrozumiałe, że muszą być) zostały na podstawach, a wektory usunięto. Wektory to przy dowodach przedszkole. Nie wiem czemu usunięto tez większość zagadnień z wielomianów, chociaż nawet słabsi uczniowie ogarniali tw. Bezouta, dzielenie wielomianów, schemat Hornera i nierówności wielomianowe. Wielomiany to dla wielu uczniów, nawet słabych, był fajny dział. A na pewno im to szło lepiej niż dowody. Usunięto też kombinatorykę z rachunku prawdopodobieństwa, czyli DE FACTO PODSTAWĘ RACHUNKU PRAWDOPODOBIEŃSTWA. Jak na ironię na poziomie podstawowym mamy prawdopodobieństwo BEZ PODSTAW. Nie wiem, czy śmiać się z tego, czy raczej płakać

Gustlik: Oto jeden z dowodów na prostotę rachunku wektorowego − zadanie 33 z matury poprawkowej na poziomie PODSTAWOWYM z sierpnia 2013 r. Rozwiązanie Jakuba, który użył metody tzw. "podstawowej", czyli trudniejszej, bo użył tylko wzorów z tzw. "podstaw": https://matematykaszkolna.pl/strona/3975.html Nawet dla dobrego ucznia jest liczenia na co najmniej 20 minut, pisania na co najmniej całą stronę A4, a w szkole to zajęłoby chyba trzy tablice w klasie i jeszcze trzeba byłoby pisać na ścianie. Do tego przy takiej ilości obliczeń łatwo o pomyłkę. Rozwiązanie moje − za pomocą wyznacznika wektorów: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3975 Kilka linijek, liczenia na co najwyżej kilka minut i po sprawie. Tą metodą nawet słaby uczeń zrobi szybciej, niż mocny uczeń metodą tzw. "podstawową". Proszę porównać. Wg mnie ta "podstawowa" metoda jest właśnie na rozszerzenia i to jedynie jako ciekawostka, a "rozszerzona" na podstawy. Każdy, komu pokazałem te dwa sposoby, się ze mną zgadzał.

Janek191: Powinno być : Z prostopadłości wektorów: → → AC i BC itd.