Trapez sevixy: YushokU: Rozpatrujemy wszystkie trapezy, wpisane w okrąg o promieniu 12 w taki sposób, że podstawa trapezu jest średnicą okręgu. Oblicz długości boków tego z rozpatrywanych trapezów, który ma największe pole. Widziałam już rysunek do tego zadania (https://matematykaszkolna.pl/forum/rysunek108758.png)

	2*6*6*sinα
co z tym dalej zrobić? Obliczyć pole trapezu jako suma pól tych trójkatów, tzn
	2

	6*6*sinβ
+		i z tego jakoś liczyć pochodną?
	2

Kompletnie nie wiem jak się za to zabrać, w innych zadaniach optymalizacyjnych od CKE było zawsze wiecej danych...

Tadeusz: ... wyrażaj wszystko za pomocą funkcji jednego kąta i długości dolnej podstawy

sevixy: więc sinβ mogę zapisać jako sin(180−2α) i dalej pochodną?

Tadeusz: ... pomagać czy poradzisz ?

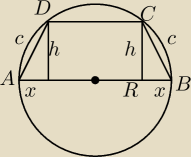
YushokU: wiemy, że ten trapez jest równoramienny. R=12 CD=2R−2x AB=2R AB+CD=AD+BC 4R−2x=2c c=2R−x h²=c²−x² h²=4R²−4Rx Mamy wszystko co nam potrzeba Jeszcze dziedzina. x∊(0,R) P(x)=(2r−x)*2√R²−4Rx Dalej pochodna i tyle. To da się jakoś łatwiej na pewno zrobić, coś sobie źle tu pokombinowałem, bo tego pierwiastka nie powinno tu być, ale tak też wyjdzie.

Tadeusz:

l
	=cosα ⇒ l=24cosα
24

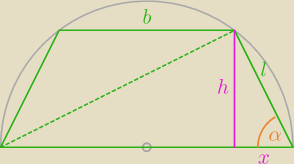
h
	=sinα ⇒ h=lsinα=24sinαcosα
l

x
	=cosα ⇒ x=lcosα=24cos2α
l

b=24−48cos^α P=....

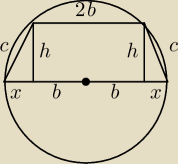
YushokU: Ojejku, przepraszam. Przecież mam do dyspozycji to R=12. Zamotałem. Chciałem szybko i nie wyszlo. Spójrz na obrazek i naśladuj to co tam zrobiłem. b+x=12 x=12−b 2b+x=c h²=c²−x² .... Wyjdzie, zapewniam. Ja już lecę!

Tadeusz: oj ....skiksowało przy b b=24−48cos²α

	24+24−48cos2α
P=		*24sinαcosα
	2

P=576sin³αcosα pochodna i ostatecznie P_max dla α=60^o

fifol: yushoku napewno 2b+x=c?

YushokU: Spitoliłem, przyznaje sie. Cały czas liczyłem dla opisanego. Wlasnie leżę w łóżku i zastanawiałem sie co ja tam narobiłem. Przepraszam, to przez maturę

sevixy: DObra, mniejsza z tym, mam nadzieję, że jednak dadzą typowe zadanie optymalizacyjne jak na próbnej

Kacper: A co tu nietypowego?

sevixy: Szczerze mówiąc nigdy nie robiłam tego typu zadania, które bazowałoby na funkcjach trygonometrycznych a jeśli chodzi o sposób robienia na samych literkach to w tym przypadku trochę się gubię. Ale wiem, że to moja wina, nie zrobiłam wystarczająco dużo zadań optymalizacyjnych, przyznaję się

Benny: Kacper możesz rozpisać jak będzie wyglądała pochodna Tadeusza?

Tadeusz: to popatrz na mój rysunek ... zauważ podobieństwo trójkątów ... wynika z niego

x		l
	=
l		24

Dalej możesz wszystko czyli b i h wyznaczyć np za pomocą l

Tadeusz: P=576sin³αcosα P'=576(3sin²αcos*cosα−sin⁴α) P'=0 3sin²αcos²α−sin⁴α=0 sin²α(3cos²α−sin²α)=0 sinα=0 − nie spełnia warunków zadania

	1
3cos2α−(1−cos2α)=0 ⇒ 4cos2α=1 ⇒ cos2α=
	4

i wszystko jasne −

Benny: Myślałem, że tą pochodną się jakoś bardziej skomplikowanie liczy, a tu jest po prostu zwykła pochodna iloczynu? P=sin³α*cosα P'=(sin³α)'*cosα+(cosα)'*sin³α P'=3*sin^α*cosα*cosα−sinα*sin³α sin³α − funkcją wewnętrzną jest sinus, a zewnętrzną sin³ czy jak?

Tadeusz: ... przecież dobrze rozpisałeś −

Benny: Hmm, może inaczej sin³x mogę zapisać jako y³ (y³)'=3y²*y'=3*sin²x*cosx tak jest dobrze?