udowodni to ktoś? edna: Wykaż,że jeżeli α,β są kątami wewnętrznymi trójkąta,to sinα+sinβ>sin(α+β)

Mila:

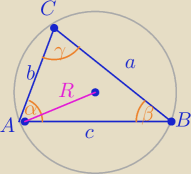
a		b		c
	=		=		=2R
sinα		sinβ		sinγ

a+b>c /:(2R) suma dwóch boków jest większa od trzeciego R −promien okręgu opisanego na Δ

a		b		c
	+		>		⇔ z tw. sinusów, że:
2R		2R		2r

sinα+sinβ>sin(180−(α+β))⇔ sinα+sinβ>sin(α+β) cnw