optymalizacjaaa fifi: zadanie optymalizacyjne za 7punktow Dana jest parabola o rownaniu y= −x²+10x−9. Rozpatrujemy wszystkie prostokaty, ktorych dwa sasiednie wierzcholki o dodatnich wspolrzednych leza na tej paraboli zas dwa pozostale wierzcholki leza na osi OX. Wyznacz wspolrzedne wierzcholkow tego z prostokatow o podanej wlasnosci ktory ma najwieksze pole. Oblicz to pole. chodzi mi glownie o oznaczenie tak aby miec jedna zmienna

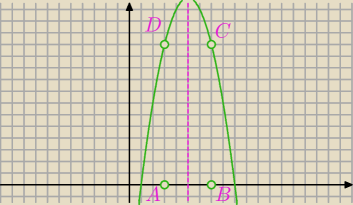
Tadeusz: x_w=5 x=5 jest osią symetrii Twojej paraboli Jeśli B=(5+b, 0) C=[5+b, −(5+b)²+10(5+b)−9] A=(5−b, 0) |AB|=2b P=2b*[−(5+b)²+10(5+b)−9] P=2b(−25−10b−b²+50+10b−9) P=2b(−b²+16) P=−2b³+32b P'=−6b²+32 P'=0 ... itd

fifi: ok rozumiem wspolrzedne A i B ale nie moge zrozumiec wspolrzednej y w punkcie C, dalej juz wiem co i jak. i ogolnie dzieki za pomoc

Tadeusz: y_c=f(x_c) a skoro x_c=5+b to y_c=−(5+b)²+10(5+b)−9

fifi: oO dzieki juz wiem wszystko

Tadeusz: oczywiście można nie wprowadzać tego b Wtedy B=(x_b, 0) podstawa |AB|=2(x_B−5) |BC|=−x_B²+10xB−9 P=2(x_B−5)(−x_B²+10x_B−9) P=