nierowjosc z modulem
filoo: Wyznacz najwieksza liczbę całkowitą spełniająca nierówność lx+5l<lx+1l
7 maj 17:40
filoo: Przykładowe do rozszerzenia jutro
7 maj 17:41
Benny: Odpowiedź masz? wyszło mi −4.
7 maj 17:48
Eta:
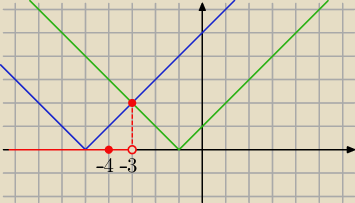
7 maj 17:48
filoo: No fajnie a można rachunkowo
7 maj 18:27
ICSP: Podnieś obustronnie do kwadratu. Możesz to zrobić ponieważ obie strony są dodanie.
7 maj 18:28
filoo: O dzięki teraz już fajnie wyszło rachunkiem

7 maj 18:33
PW: Sposób bez rysowania i bez podnoszenia do kwadratu:
Dzielimy obie strony przez dodatnie |x+1| (gdyby było równe zeru, to rozwiązań nie ma):
Widać, że dla x > −1 rozwiązań nie ma (ułamek jest dodatni), natomiast dla x < −1 mnożymy przez
ujemne (x+1):
−2(x+1)
> 4
> 0, x < −1
−2x > 6, x < −1
x < − 3, x < −1
− i też widać, że szukanym rozwiązaniem jest −4.
7 maj 23:12
Eta:
"bez rysowania i podnoszenia do kwadratu"

|x+5|<|x+1| ⇔ (x+5>x+1 i −x−5<x+1) ⇒ x<−3
x= −4 −−największa liczba całkowita ∊( −
∞, −3)
7 maj 23:25
Benny: Pani
Eto, wydaje mi się że coś jest nie tak w tym nawiasie

7 maj 23:37
Eta:
Racja

źle wpisałam minusy ( nie po tej stronie ... pora zmienić okulary

.... (x+5>x+1 i x+5< −x−1) ⇒ 2x<−6 ⇒x<−3
teraz jest ok

7 maj 23:49
Benny: 
7 maj 23:49


 |x+5|<|x+1| ⇔ (x+5>x+1 i −x−5<x+1) ⇒ x<−3
x= −4 −−największa liczba całkowita ∊( −∞, −3)
|x+5|<|x+1| ⇔ (x+5>x+1 i −x−5<x+1) ⇒ x<−3
x= −4 −−największa liczba całkowita ∊( −∞, −3)

 źle wpisałam minusy ( nie po tej stronie ... pora zmienić okulary
źle wpisałam minusy ( nie po tej stronie ... pora zmienić okulary  .... (x+5>x+1 i x+5< −x−1) ⇒ 2x<−6 ⇒x<−3
teraz jest ok
.... (x+5>x+1 i x+5< −x−1) ⇒ 2x<−6 ⇒x<−3
teraz jest ok
