pochodne Stanisław: Dana jest funkcja o równaniu f(x)=4x³−2x+1 Uzasadnij, że prosta o równaniu y=10x+9 jest styczna do wykresu funkcji. Można to uzasadnić przyrównując te dwie funkcje i udowodnić, że mają jeden punkt wspólny ?

Aerodynamiczny: Nie.

J: f'(x) = 12x² − 2 f'(x) = 10 ⇔ 12x² − 2 = 10 ⇔ 12x² = 12 ⇔ x = 1 lub x = −1 ( punkty styczności)

Frost: https://matematykaszkolna.pl/strona/379.html

Stanisław: to dlatego, że mogą się jeszcze gdzieś przeciąć, tak ?

Stanisław:

J: nie .. styczna ma tylko jeden punkt wspólny z krzywą

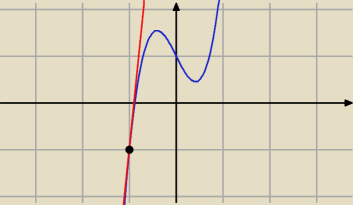
Bogdan: Na rysunku Stanislawa widać, że styczna może mieć więcej punktów z krzywą, nieprawdziwe jest więc stwierdzenie J, że styczna ma tylko jeden punkt z krzywą, a może nie?

Stanisław: jak to dlaczego nie mogą się przecinać ?

Stanisław: właśnie

Stanisław: czyli już ogarniam, dzięki

J: Racja Bogdan ... może

Bogdan: 4x³ − 2x + 1 = 10x + 9 ⇒ 4x³ − 12x − 8 = 0 ⇒ (x + 1)²(x − 2) = 0 Równanie ma jeden pierwiastek podwójny x = −1 oraz jeden pierwiastek pojedynczy x = 2. Dla x = −1 prosta y = 10x + 9 jest styczna do wykresu funkcji f(x) = 4x³ − 12x − 8

Bogdan: Inny sposób: Jeśli prosta y = 10x + 9 jest styczna do wykresu funkcji f(x) = 4x³ − 2x + 1, to f'(x₀) = 10 f'(x) = 12x² − 2, 12x² − 2 = 10 ⇒ x² = 1 ⇒ x = −1 lub x = 1 dla x = −1: f(−1) = 4*(−1) − 2*(−1) + 1 = −1 oraz dla prostej y = 10*(−1) + 9 = −1 więc punktem styczności jest punkt (−1, −1) dla x = 1: f(1) = 4*1 − 2*1 + 1 = 3 oraz dla prostej y = 10*1 + 9 = 19 więc dla x = −1 prosta y = 10x + 9 nie jest styczna do wykresu funkcji f(x)

pigor: ... . Dana jest funkcja o równaniu f(x)= 4x³−2x+1. Uzasadnij, że prosta o równaniu y=10x+9 jest styczna do wykresu funkcji. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− to może jeszcze do ... szuflady Mai, pozwolę sobie tak: z warunków zadania i własności stycznej powinien istnieć punkt wspólny wykresu funkcji f i danej prostej S=(a,b) taki, że f ' (a)= 10 i f(a)=4a³−2a+1= b i b=10a+9 ⇒ ⇒ 12a²−2=10 i 4a³−2a+1=10a+9 ⇔ |a|=1 i 4a³−12a−8= 0 ⇔ ⇔ (a= −1 v a=1) i a³−3a−2= 0 ⇔ ⇔ (a= −1 i −1+3−2= 0) v (a= 1 i 1−3−2= 0) ⇔ ⇔ (a= −1 i b= −1) v ∅ ⇔ S= (−1,−1) . c.n.uz. ...