Eta:
 2 sposób
2 sposób
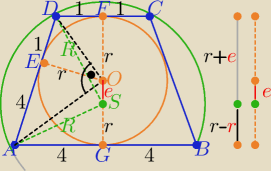
Z trójkąta prostokątnego AOD : r
2=4*1 ⇒ r=2 , |DE|=1 , |AE|=4
Szukana odległość : |SO|=e , e>0 ,|FG|=2r=4 i |FS|=r+e= 2+e , ||SG|=r−e =2−e , e<2
Z tw. Pitagorasa
w ΔAGS : (2−e)
2+4
2=R
2 i ΔDFS : (2+e)
2+1=R
2
| | 15 | |
to 4−4e+e2+16= 4+4e+e2+1⇒ 8e=15 ⇒ e= |
| |
| | 8 | |

pigor: .., no to jeszcze np. tak :
z warunków zadania i tw.o okręgu wpisanym (opisanym) w(na)
czworokącie 5 − długość ramienia trapezu, a więc h=4 − długość
jego wysokości, czyli
r=2 długość promienia okręgu wpisanego,
w ten trapez, teraz
umieszczę dany trapez na płaszczyźnie z układem osi xOy tak,
że punkt (0,0) − środkiem podstawy dolnej danego trapezu, a oś
Oy − oś symetrii tego trapezu, to z warunków zadania :
A=(4,0), B=(−4,0), C=(1,4), D=(4,0) − współrzędne wierzchołków
trapezu i E=(−1.5, 2) − środek przekątnej AC, to wektor AC=[5,4],
zatem równanie symetralnej boku ΔABC (przekątnej trapezu)
AC: 5(x+1.5)+4(y−2)=0 /*2 ⇔ 10x+8y=1, która z symetralną
boku AB ΔABC o równaniu x=0 "daje" środek S
R= (0,
18) okręgu
opisanego na ΔABC, a zarazem na danym trapezie, ale
S
r=(,0,2) − − środek okręgu wpisanego w dany trapez, to
|SrSR| =| 2−
18 | =
158 = 1
78 =
1,875 − szukana odległość.

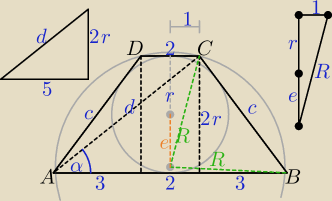 2c = 8 + 2 ⇒ c = 5, 2r = √25 − 9 = 4 ⇒ r = 2
2c = 8 + 2 ⇒ c = 5, 2r = √25 − 9 = 4 ⇒ r = 2
 2 sposób
Z trójkąta prostokątnego AOD : r2=4*1 ⇒ r=2 , |DE|=1 , |AE|=4
Szukana odległość : |SO|=e , e>0 ,|FG|=2r=4 i |FS|=r+e= 2+e , ||SG|=r−e =2−e , e<2
Z tw. Pitagorasa
w ΔAGS : (2−e)2+42=R2 i ΔDFS : (2+e)2+1=R2
2 sposób
Z trójkąta prostokątnego AOD : r2=4*1 ⇒ r=2 , |DE|=1 , |AE|=4
Szukana odległość : |SO|=e , e>0 ,|FG|=2r=4 i |FS|=r+e= 2+e , ||SG|=r−e =2−e , e<2
Z tw. Pitagorasa
w ΔAGS : (2−e)2+42=R2 i ΔDFS : (2+e)2+1=R2




