Mam problem. Nikt: Mam problem z tą granicą. limx→5 √x²−9/(x−5) Pierwiastek jest dzielony x−5. Będę bardzo wdzięczny, jak ktoś pokaże mi jak to zrobić.

Janek191:

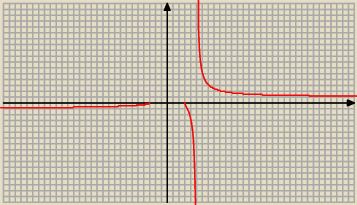
	√x2 − 9
f(x) =		, x ≠ 5
	x − 5

więc lim f(x) = + ∞ x→5⁺ oraz lim f(x) = − ∞ x → 5⁻

Nikt: Coś mi się chyba przypomina.

	a2−b2
Można zacząć w ten sposób ? (a−b)(a+b)=a2−b2 (a−b)=
	a+b

Janek191: Licznik dąży do 4, a mianownik dąży do 0 , więc ułamek dąży do + ∞ lub do − ∞ w zależności o tego, czy x dąży do 5 z prawej strony, czy też z lewej strony.

Nikt: Kurcze zle przepisałem, a patrzyłem do książki.

	√x2−9 −4
Powinno być lim→5
	x−5

	a2−b2
(a−b)=		i z tego policzyć.
	a+b

x2 −9 −16		1
	*		Wynik mój wychodzi 1,25.
√x2−9+4		x−5

W ten sposób ten przykład po korekcie się robi ?

Janek191: Tak